题目内容
20.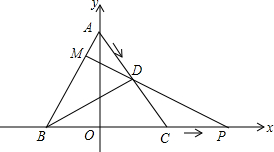 如图,将等边三角形ABC放在平面直角坐标系中,使得BC在x轴上,点A在y轴正半轴上,已知AB=4,AO=2$\sqrt{3}$,若点D从A出发沿AC向C运动,点P从C出发沿x轴正方向运动,点D、P均以每秒0.5个单位长度的速度同时开始运动,设运动时间为t,运动过程中连接PD并延长交AB于点M.
如图,将等边三角形ABC放在平面直角坐标系中,使得BC在x轴上,点A在y轴正半轴上,已知AB=4,AO=2$\sqrt{3}$,若点D从A出发沿AC向C运动,点P从C出发沿x轴正方向运动,点D、P均以每秒0.5个单位长度的速度同时开始运动,设运动时间为t,运动过程中连接PD并延长交AB于点M.(1)当∠AMD=105°时,求∠DPC的大小.
(2)当△PBM是直角三角形,求出t的值.
(3)在(2)的情况下,连接BD,此时x轴上存在点N,使得组成△BDN为等腰三角形,求出点N的坐标.
分析 (1)由等边三角形的性质得到∠ABC=∠ACB=∠CAB=60°,根据三角形的外角的性质得到∠AMD=∠ABC+∠P,代入数据即可得到结果;
(2)由已知条件△PBM是直角三角形,得到∠PMB=90°,求得∠MPB=30°,得到∠CDP=∠DPC=30°,于是得到结论;
(3)由等边三角形的性质得到BO=CO=2,BD=AO=2$\sqrt{3}$,①当BD=BN=2$\sqrt{3}$时,求得N1(-2-2$\sqrt{3}$,0),N2(2$\sqrt{3}$-2,0),②当BD=DN=2$\sqrt{3}$,解直角三角形求得N3(4.0),③当BN=DN时,解直角三角形得到N4(0,0),于是得到结论.
解答 解:(1)∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠CAB=60°,
∵∠AMD=∠ABC+∠P,
∵∠AMP=105°,
∴∠DPC=45°;
(2)∵△PBM是直角三角形,
∴PM⊥AB,
∴∠PMB=90°,
∴∠MPB=30°,
∴∠DCP=∠DPC+∠CDP,
,∴∠CDP=∠DPC=30°,
∴CD=CP=AD=$\frac{1}{2}$AC=2,
∴t=2÷0.5=4s;
(3)∵AB=AC,AO⊥BC,
∴BO=CO=2,
∵AD=CD,
∴BD⊥AC,BD=AO=2$\sqrt{3}$,
①当BD=BN=2$\sqrt{3}$时,
∴ON1=BN1+OB=2+2$\sqrt{3}$,
ON2=BN2-OB=2$\sqrt{3}$-2,
∴N1(-2-2$\sqrt{3}$,0),N2(2$\sqrt{3}$-2,0),
②当BD=DN=2$\sqrt{3}$,
∵∠DBN3=∠DN3B=30°,
∴BN3=6,
∴ON3=4,
∴N3(4.0),
③当BN=DN时,
∴∠DBN4=∠BDN4,
∴BN4=2,
∴ON4=0,
∴N4(0,0),
∴x轴上存在点N,使得△BDN为等腰三角形,点N的坐标为(-2-2$\sqrt{3}$,0)、(0,0)、(2$\sqrt{3}$-2,0)、(4,0).
点评 本题考查了等边三角形的性质,等腰三角形的判定和性质,特殊角的三角函数,解直角三角形,要根据N点的不同位置进行分类是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ | B. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | C. | $\sqrt{6}$÷2=$\sqrt{3}$ | D. | $\sqrt{8}=4$ |
| A. | 所有的有理数都可以用数轴上的点来表示 | |
| B. | 数轴上所有的点都表示有理数 | |
| C. | 数轴上找不到既不表示正数也不表示负数的点 | |
| D. | 数轴上表示-a的点一定在原点的左边 |
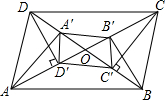 已知:如图所示,在?ABCD中,过A,C作BD的垂线垂足为A′,C′,过B,D作AC的垂线,垂足为B′,D′(AC,BD不垂直).
已知:如图所示,在?ABCD中,过A,C作BD的垂线垂足为A′,C′,过B,D作AC的垂线,垂足为B′,D′(AC,BD不垂直).