题目内容
2.有一列数-$\frac{10}{5}$,$\frac{17}{12}$,-$\frac{26}{21}$,$\frac{37}{32}$,-$\frac{50}{45}$…,则这列数的第九个数为-$\frac{61}{58}$,第n个数为(-1)n$\frac{(n+2)^{2}+1}{(n+2)^{2}-5}$.分析 分子是(n+2)2+1,分母比分子小1,奇数位置为负,偶数位置为正,由此得出第n个数为(-1)n$\frac{(n+2)^{2}+1}{(n+2)^{2}-5}$,利用规律得出答案即可.
解答 解:∵分子是(n+2)2+1,分母比分子小1,奇数位置为负,偶数位置为正,
∴这列数的第九个数为-$\frac{1{1}^{2}+1}{1{1}^{2}-5}$=-$\frac{61}{58}$,第n个数为(-1)n$\frac{(n+2)^{2}+1}{(n+2)^{2}-5}$.
故答案为:-$\frac{61}{58}$,(-1)n$\frac{(n+2)^{2}+1}{(n+2)^{2}-5}$.
点评 此题考查数字的变化规律,找出数字的运算规律与符号排列的规律,利用规律解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列计算正确的是( )
| A. | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ | B. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | C. | $\sqrt{6}$÷2=$\sqrt{3}$ | D. | $\sqrt{8}=4$ |
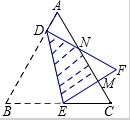 如图,将边长为3$\sqrt{3}$+3的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=$\sqrt{3}$,则重叠部分的面积为$\frac{27+9\sqrt{3}}{4}$.
如图,将边长为3$\sqrt{3}$+3的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=$\sqrt{3}$,则重叠部分的面积为$\frac{27+9\sqrt{3}}{4}$.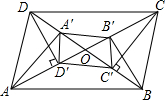 已知:如图所示,在?ABCD中,过A,C作BD的垂线垂足为A′,C′,过B,D作AC的垂线,垂足为B′,D′(AC,BD不垂直).
已知:如图所示,在?ABCD中,过A,C作BD的垂线垂足为A′,C′,过B,D作AC的垂线,垂足为B′,D′(AC,BD不垂直).