题目内容
4. 如图,在△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径的圆与斜边AB只有一个公共点,则R的值是3<r≤4或r=$\frac{12}{5}$.
如图,在△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径的圆与斜边AB只有一个公共点,则R的值是3<r≤4或r=$\frac{12}{5}$.
分析 根据直线与圆的位置关系得出相切时有一交点,再结合图形得出另一种有一个交点的情况,即可得出答案.
解答 解解:过点C作CD⊥AB于点D,
∵AC=3,BC=4.如果以点C为圆心,r为半径的圆与斜边AB只有一个公共点,
∴AB=5,
当直线与圆相切时,d=r,圆与斜边AB只有一个公共点,圆与斜边AB只有一个公共点,如图1,
∴CD×AB=AC×BC,
∴CD=r=$\frac{12}{5}$,
当直线与圆如图所示也可以有一个交点,如图2,
∴3<r≤4,
故答案为:3<r≤4或r=$\frac{12}{5}$.
点评 此题主要考查了直线与圆的位置关系,结合题意画出符合题意的图形,从而得出答案,此题比较容易漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.抛物线y=-3x2向左平移1个单位,再向下移2个单位,所得到的抛物线是( )
| A. | y=-3(x-1)2-2 | B. | y=-(x+1)2-2 | C. | y=-3(x+1)2+2 | D. | y=-3(x-)2+2 |
13.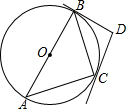 如图,AB是⊙O的直径,BD、CD分别是过⊙O上点B、C的切线,且∠BDC=100°,连接AC,则∠A的度数是( )
如图,AB是⊙O的直径,BD、CD分别是过⊙O上点B、C的切线,且∠BDC=100°,连接AC,则∠A的度数是( )
 如图,AB是⊙O的直径,BD、CD分别是过⊙O上点B、C的切线,且∠BDC=100°,连接AC,则∠A的度数是( )
如图,AB是⊙O的直径,BD、CD分别是过⊙O上点B、C的切线,且∠BDC=100°,连接AC,则∠A的度数是( )| A. | 15° | B. | 30° | C. | 40° | D. | 45° |
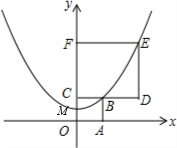 如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则$\frac{FE}{CB}$的值为1+$\sqrt{2}$.
如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则$\frac{FE}{CB}$的值为1+$\sqrt{2}$.