题目内容
2. 如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,围成长方形的鸡场除门之外四周不能有空隙.求:
如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,围成长方形的鸡场除门之外四周不能有空隙.求:(1)若墙长为18米,要围成鸡场的面积为150平方米,则鸡场的长和宽各为多少米?
(2)围成鸡场的面积可能达到200平方米吗?
(3)若墙长为a米,对建150平方米面积的鸡场有何影响?
分析 (1)先设养鸡场的宽为xm,得出长方形的长,再根据面积公式列出方程,求出x的值即可,注意x要符合题意;
(2)先设养鸡场的宽为xm,得出长方形的长,再根据面积公式列出方程,判断出△的值,即可得出答案;
(3)根据实际问题当0<a<15时,当15≤a<20时,当a≥20时,三种情况进行讨论,得出符合条件的值即可.
解答 解:(1)设养鸡场的宽为xm,根据题意得:
x(33-2x+2)=150,
解得:x1=10,x2=7.5,
当x1=10时,33-2x+2=15<18,
当x2=7.5时33-2x+2=20>18,(舍去),
则养鸡场的宽是10m,长为15m.
(2)设养鸡场的宽为xm,根据题意得:
x(33-2x+2)=200,
整理得:2x2-35x+200=0,
△=(-35)2-4×2×200=1225-1600=-375<0,
因为方程没有实数根,
所以围成养鸡场的面积不能达到200m2;
(3)当0<a<15时,不能围成一个长方形养鸡场;
当15≤a<20时,可以围成一个长方形养鸡场;
当a≥20时,可以围成一个长方形养鸡场.
点评 此题考查了一元二次方程的应用,读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程是解题的关键,注意宽的取值范围.

练习册系列答案
相关题目
13.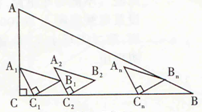 如图,在△ABC中,∠C=90°,AC=2,BC=4.△A1B1C1、△A2B2C2、△A3B3C3、…、△AnBnCn是n个相同的等腰直角三角形,其直角顶点C1、C2、C3、…、Cn都在CB边上,点A1在AC上,A2C2经过点B1且平行于A1C1,A3C3经过点B2且平行于A2C2,…,AnCn过点Bn-1且平行于An-1Cn-1,且A1C=2CC1.当n=7时,点B7正好落在AB边,则这个小的等腰直角三角形的直角边长为( )
如图,在△ABC中,∠C=90°,AC=2,BC=4.△A1B1C1、△A2B2C2、△A3B3C3、…、△AnBnCn是n个相同的等腰直角三角形,其直角顶点C1、C2、C3、…、Cn都在CB边上,点A1在AC上,A2C2经过点B1且平行于A1C1,A3C3经过点B2且平行于A2C2,…,AnCn过点Bn-1且平行于An-1Cn-1,且A1C=2CC1.当n=7时,点B7正好落在AB边,则这个小的等腰直角三角形的直角边长为( )
 如图,在△ABC中,∠C=90°,AC=2,BC=4.△A1B1C1、△A2B2C2、△A3B3C3、…、△AnBnCn是n个相同的等腰直角三角形,其直角顶点C1、C2、C3、…、Cn都在CB边上,点A1在AC上,A2C2经过点B1且平行于A1C1,A3C3经过点B2且平行于A2C2,…,AnCn过点Bn-1且平行于An-1Cn-1,且A1C=2CC1.当n=7时,点B7正好落在AB边,则这个小的等腰直角三角形的直角边长为( )
如图,在△ABC中,∠C=90°,AC=2,BC=4.△A1B1C1、△A2B2C2、△A3B3C3、…、△AnBnCn是n个相同的等腰直角三角形,其直角顶点C1、C2、C3、…、Cn都在CB边上,点A1在AC上,A2C2经过点B1且平行于A1C1,A3C3经过点B2且平行于A2C2,…,AnCn过点Bn-1且平行于An-1Cn-1,且A1C=2CC1.当n=7时,点B7正好落在AB边,则这个小的等腰直角三角形的直角边长为( )| A. | $\frac{1}{7}$ | B. | $\frac{\sqrt{5}}{7}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{8\sqrt{5}}{5}$ |
17.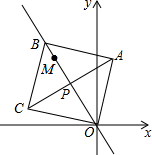 如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )
如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )
 如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )
如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )| A. | ($\frac{3}{2}$,$\frac{65}{6}$) | B. | ($\sqrt{7}$,11) | C. | (2,2$\sqrt{31}$) | D. | ($\frac{8}{5}$,$\frac{56}{5}$) |
14.已知-4xay与x2yb是同类项,则a+b的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
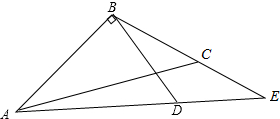 已知,如图,△ABC中,BD⊥AB于点B,AD的延长线交BC于点E.若∠CAE=∠CBD,∠EAB-∠BCA=10°,求出∠BAD的度数.
已知,如图,△ABC中,BD⊥AB于点B,AD的延长线交BC于点E.若∠CAE=∠CBD,∠EAB-∠BCA=10°,求出∠BAD的度数.