题目内容
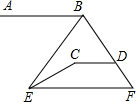
如图，AB∥CD，且∠A=25°，∠C=45°，则∠E的度数是（ ）| A、60° | B、70° |
| C、80° | D、110° |
考点：平行线的性质
专题：
分析：过点E作EF∥AB，根据两直线平行，内错角相等可得∠AEF=∠A，∠CEF=∠C，然后根据∠AEC=∠AEF+∠CEF计算即可得解．
解答：
解：过点E作EF∥AB，
∵AB∥CD，
∴AB∥EF∥CD，
∴∠AEF=∠A，∠CEF=∠C，
∴∠AEC=∠AEF+∠CEF=25°+45°=70°．
故选B．
解：过点E作EF∥AB，∵AB∥CD，
∴AB∥EF∥CD，
∴∠AEF=∠A，∠CEF=∠C，
∴∠AEC=∠AEF+∠CEF=25°+45°=70°．
故选B．
点评：本题考查了平行线的性质，熟记性质是解题的关键，此类题目，难点在于过拐点作平行线．
练习册系列答案
名校课堂系列答案
相关题目
如图，在△ACE和△DBF中，点A，B，C，D在一条直线上，∠A=∠D，AE=DF．在下列条件中随机抽取一个作为补充条件：①∠E=∠F；②AB=CD；③CE=BF；④CE∥BF．能使△ACE≌△DBF的概率是
如图，点O是直线AD上一点，射线OC、OE分别是∠AOB、∠BOD的平分线，若∠AOC=25°，则∠BOE=
如图，AB∥CD∥EF，∠ABE=50°，∠ECD=160°，则∠BEC的度数为（ ）| A、20° | B、25° |
| C、30° | D、35° |
一辆汽车匀速通过某段公路，所需时间t（h）与行驶速度v（km/h）满足函数关系t=| k |
| v |
| A、40，80 |
| B、40，60 |
| C、80，80 |
| D、80，60 |
如图，P在∠AOB内，点M、N分别是点P关于AO、BO的对称点，如果△PEF的周长为15，则MN的长为（ ）| A、15 | B、16 | C、17 | D、18 |
已知反比例函数y=
（k＞0）的图象上有两点A（-2，y1），B（2，y2），则y1-y2的值是（ ）
| k |
| x |
| A、正数 | B、负数 | C、0 | D、无法确定 |
如图，直线y1=k1x+a与y2=k2x+b的交点坐标为（1，2），则使y2＜y1的取值范围为（ ）| A、x＞1 | B、x＞2 |
| C、x＜1 | D、x＜2 |