题目内容
6.已知α,β是方程2x2-3x+1=0的两个根,则α+β=$\frac{3}{2}$,α•β=$\frac{1}{2}$,α2β+αβ2=$\frac{3}{4}$.分析 先根据根与系数的关系直接得到α+β=$\frac{3}{2}$,α•β=$\frac{1}{2}$,再利用因式分解得到α2β+αβ2=αβ(α+β),然后利用整体代入的方法计算.
解答 解:根据题意得α+β=$\frac{3}{2}$,α•β=$\frac{1}{2}$,
α2β+αβ2=αβ(α+β)=$\frac{1}{2}$×$\frac{3}{2}$=$\frac{3}{4}$.
故答案为$\frac{3}{2}$,$\frac{1}{2}$,$\frac{3}{4}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
17.如果$\frac{\sqrt{x-1}}{\sqrt{x+1}}$有意义,那么x的取值范围是( )
| A. | x≥-1 | B. | x≠-1 | C. | x≥1 | D. | x>-1 |
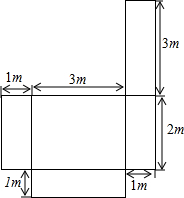 如图是一张铁片.
如图是一张铁片.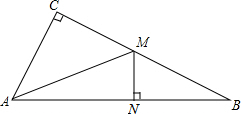 如图,在Rt△ABC中,∠C=90,AM是中线,MN⊥AB,垂足为点N,求证:AN2-BN2=AC2.
如图,在Rt△ABC中,∠C=90,AM是中线,MN⊥AB,垂足为点N,求证:AN2-BN2=AC2.