题目内容
2.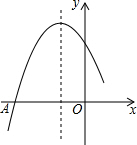 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c=0;④5a<b.
其中正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由函数图象可知b2-4ac>0,故b2>4ac成立,则①正确;由对称轴x=-1知,$-\frac{b}{2a}=-1$,故2a=b,又因函数图象开口向下知a<0,故2a+b<0,则②错误;由题目可知函数图象与x轴的另一个交点是(1,0),故a+b+c=0,则③正确;由对称轴x=-1知,$-\frac{b}{2a}=-1$,故2a=b,又因函数图象开口向下知a<0,故5a<2a,即5a<b成立,故④正确.
解答 解:A.由函数图象可知b2-4ac>0,故b2>4ac成立,则①正确;由对称轴x=-1知,$-\frac{b}{2a}=-1$,故2a=b,又因函数图象开口向下知a<0,故2a+b<0,则②错误;由题目可知函数图象与x轴的另一个交点是(1,0),故a+b+c=0,则③正确;由对称轴x=-1知,$-\frac{b}{2a}=-1$,故2a=b,又因函数图象开口向下知a<0,故5a<2a,即5a<b成立,故④正确.故选项错误;
B.由函数图象可知b2-4ac>0,故b2>4ac成立,则①正确;由对称轴x=-1知,$-\frac{b}{2a}=-1$,故2a=b,又因函数图象开口向下知a<0,故2a+b<0,则②错误;由题目可知函数图象与x轴的另一个交点是(1,0),故a+b+c=0,则③正确;由对称轴x=-1知,$-\frac{b}{2a}=-1$,故2a=b,又因函数图象开口向下知a<0,故5a<2a,即5a<b成立,故④正确.故选项错误;
C.由函数图象可知b2-4ac>0,故b2>4ac成立,则①正确;由对称轴x=-1知,$-\frac{b}{2a}=-1$,故2a=b,又因函数图象开口向下知a<0,故2a+b<0,则②错误;由题目可知函数图象与x轴的另一个交点是(1,0),故a+b+c=0,则③正确;由对称轴x=-1知,$-\frac{b}{2a}=-1$,故2a=b,又因函数图象开口向下知a<0,故5a<2a,即5a<b成立,故④正确.故选项正确;
D.由函数图象可知b2-4ac>0,故b2>4ac成立,则①正确;由对称轴x=-1知,$-\frac{b}{2a}=-1$,故2a=b,又因函数图象开口向下知a<0,故2a+b<0,则②错误;由题目可知函数图象与x轴的另一个交点是(1,0),故a+b+c=0,则③正确;由对称轴x=-1知,$-\frac{b}{2a}=-1$,故2a=b,又因函数图象开口向下知a<0,故5a<2a,即5a<b成立,故④正确.故选项错误;
故选C.
点评 本题考查二次函数图象与系数之间的关系,只要会看函数图象,知道函数图象与x轴的交点关于对称轴对称,问题就可得以解决.

 阅读快车系列答案
阅读快车系列答案 如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )| A. | 1cm | B. | 2cm | C. | 4cm | D. | 6cm |
 如图,在直角坐标系中,△ABC为等腰直角三角形,且AB、BC的长分别是方程x2-10x+m=0的两个根.
如图,在直角坐标系中,△ABC为等腰直角三角形,且AB、BC的长分别是方程x2-10x+m=0的两个根.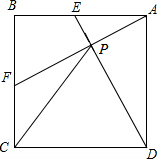 在正方形ABCD中,E、F分别是AB、BC的中点,AF和DE交于点P,求证:CP=CD.
在正方形ABCD中,E、F分别是AB、BC的中点,AF和DE交于点P,求证:CP=CD.