题目内容
14.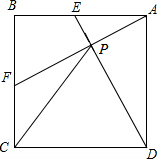 在正方形ABCD中,E、F分别是AB、BC的中点,AF和DE交于点P,求证:CP=CD.
在正方形ABCD中,E、F分别是AB、BC的中点,AF和DE交于点P,求证:CP=CD.
分析 延长AF、CD交于点G,先证△ABF≌△DAE,再证△FCG≌△FBA得GC=CD由直角三角形中斜边中线等于斜边的一半,可得Rt△PGD中CP=$\frac{1}{2}$GD,即PC=CD.
解答 证明:延长AF、CD交于点G,
∵点E、F分别是正方形ABCD的边AB和BC的中点,
∴AB=AD,∠ABF=∠DAE,BF=AE,
在△ABF与△DAE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠ABF=∠DAE}\\{BF=AE}\end{array}\right.$,
∴△ABF≌△DAE(SAS),
∴∠BFA=∠AED.
∵∠BFA+∠EAP=90°,
∴∠AED+∠EAP=90°,
∴∠EPG=∠AED+∠EAP=90°.
又∵BF=FC,∠GFC=∠AFB,∠FCG=∠FBA,
在△FCG与△FBA中,
$\left\{\begin{array}{l}{∠FCG=∠FBA}\\{∠GFC=∠AFB}\\{BF=FC}\end{array}\right.$,
∴△FCG≌△FBA(AAS),
∴GC=AB.
∵CD=AB,
∴AB=GC.
∴PC是直角△GPD斜边GD上的中线,
∴PC=$\frac{1}{2}$GD,
即PC=CD.
点评 本题考查了正方形各边长相等、各内角为直角的性质,全等三角形的判定和对应边相等的性质,直角三角形斜边中线长为斜边长一半的性质,本题中求证△ABF≌△DAE是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
4.下列说法正确的是( )
| A. | 三角形的三个外角的和是180° | |
| B. | 三角形的一个外角大于任何一个内角 | |
| C. | 有两边和它们的夹角对应相等的两个三角形全等 | |
| D. | 如果两个三角形不全等,那么这两个三角形的面积一定不相等 |
2.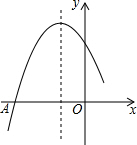 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:
①b2>4ac;②2a+b=0;③a+b+c=0;④5a<b.
其中正确的个数有( )
 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c=0;④5a<b.
其中正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.在第六次全国人口普查中,巴市常住人口约100万人,其中65岁及以上人口占9.2%,则该市65岁及以上人口用科学记数法表示约为( )
| A. | 0.92×104 | B. | 9.2×104 | C. | 9.2×105 | D. | 9.2×106 |
3.(-0.125)2015×82015+(-1)2015+(-1)2016的值是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
4.下列逆命题成立的是( )
| A. | 若两数相等,则它们绝对值相等 | |
| B. | 如果两个实数是正数,它们的积是正数 | |
| C. | 等边三角形是锐角三角形 | |
| D. | 线段垂直平分线上的点与这条线段两个端点的距离相等 |