题目内容
13.已知a=$\sqrt{2}$,b=$\sqrt{2}$+1,先化简,再求值($\frac{{b}^{2}}{a-b}$+$\frac{{a}^{2}}{b-a}$)÷($\frac{1}{a}$+$\frac{1}{b}$).分析 先算括号里面的,再算除法,最后把a,b的值代入进行计算即可
解答 解:原式=$\frac{{b}^{2}-{a}^{2}}{a-b}$÷$\frac{a+b}{ab}$
=$\frac{-(a+b)(a-b)}{a-b}$•$\frac{ab}{a+b}$
=-(a+b)•$\frac{ab}{a+b}$
=-ab,
当a=$\sqrt{2}$,b=$\sqrt{2}$+1时,原式=-$\sqrt{2}$($\sqrt{2}$+1)=-2-$\sqrt{2}$.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.

练习册系列答案
相关题目
18.若关于x的一元二次方程(2k-1)x2-8x+6=0没有实数根,则k的最小整数值是( )
| A. | -1 | B. | 2 | C. | 3 | D. | 4 |
2. 如图,已知直线AB∥CD,∠DCE=70°,∠A=30°则∠E的度数是( )
如图,已知直线AB∥CD,∠DCE=70°,∠A=30°则∠E的度数是( )
 如图,已知直线AB∥CD,∠DCE=70°,∠A=30°则∠E的度数是( )
如图,已知直线AB∥CD,∠DCE=70°,∠A=30°则∠E的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 70° |
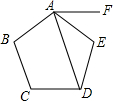 如图,过正五边形ABCDE的顶点A作AF∥CD,连结AD,则∠FAD=72度.
如图,过正五边形ABCDE的顶点A作AF∥CD,连结AD,则∠FAD=72度.