题目内容
10.解方程:①4x(2x+1)=3(2x+1)
②(x+3)(x-1)=5.
分析 ①先移项得到4x(2x+1)-3(2x+1)=0,然后利用因式分解法解方程;
②先把方程化为一般式,然后利用因式分解法解方程.
解答 解:①4x(2x+1)-3(2x+1)=0,
(2x+1)(4x-3)=0,
2x+1=0或4x-3=0,
所以x1=-$\frac{1}{2}$,x2=$\frac{3}{4}$;
②x2+2x-8=0,
(x-2)(x+4)=0,
x-2=0或x+4=0,
所以x1=2,x2=-4.
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.也考查了直接开平方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.一直角三角形的两直角边长为3和4,则第三边长为( )
| A. | $\sqrt{7}$ | B. | 5 | C. | $\sqrt{7}$或5 | D. | 7 |
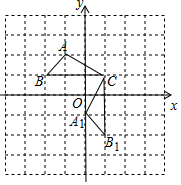 已知如图,在直角坐标平面内,△ABC的三个顶点的坐标分别为A(-1,2),B(-2,1)(正方形网格中每个小正方形的边长是1个单位长度).
已知如图,在直角坐标平面内,△ABC的三个顶点的坐标分别为A(-1,2),B(-2,1)(正方形网格中每个小正方形的边长是1个单位长度).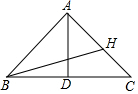 如图,在△ABC中,AB=10,BC=12,BC边上的中线AD=8.
如图,在△ABC中,AB=10,BC=12,BC边上的中线AD=8.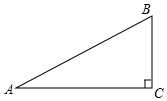 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.