题目内容
18.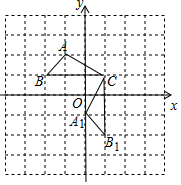 已知如图,在直角坐标平面内,△ABC的三个顶点的坐标分别为A(-1,2),B(-2,1)(正方形网格中每个小正方形的边长是1个单位长度).
已知如图,在直角坐标平面内,△ABC的三个顶点的坐标分别为A(-1,2),B(-2,1)(正方形网格中每个小正方形的边长是1个单位长度).(1)△A1B1C1是△ABC绕点C逆时针旋转90度得到的,B1的坐标是(1,-2);
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).
分析 (1)由旋转的性质即可得;
(2)根据勾股定理求得半径AC的长,由扇形面积公式可得答案.
解答 解:(1)由图可知,△A1B1C1是△ABC绕点C逆时针旋转90度得到的,B1的坐标是(1,-2),
故答案为:C,90,(1,-2);
(2)∵AC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴线段AC旋转过程中所扫过的面积$\frac{90°•π•(\sqrt{5})^{2}}{360°}$=$\frac{5π}{4}$.
点评 本题主要考查坐标与图形的变化-旋转和扇形的面积的计算,熟练掌握旋转的定义和扇形的面积公式是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
8.正方形ABCD的对角线AC的长是12cm,则边长AB的长是( )
| A. | 6$\sqrt{2}$ | B. | 2$\sqrt{12}$ | C. | 6 | D. | 8 |
13.下列汽车标志中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
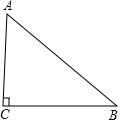 如图,已知△ABC,∠C=90°,AC<BC.D为BC上一点,且到A,B两点的距离相等.
如图,已知△ABC,∠C=90°,AC<BC.D为BC上一点,且到A,B两点的距离相等.