题目内容
20.背面完全一样的四张卡片上分别写有数字2、5、0、3,从中任取一张,并用这张卡片上的数字与1的差作为k值,抽到能使一元二次方程(k+2)x2-2$\sqrt{3}$x+1=0有解的卡片概率是$\frac{1}{2}$.分析 根据一元二次方程的定义和判别式的意义得到k+2≠0且△=(2$\sqrt{3}$)2-4(k+2)≥0,解得k≤1且k≠-2,由于从四张卡片中任取一张上只有写有数字2,0的满足条件,然后根据概率的定义计算抽到能使一元二次方程(k+2)x2-2$\sqrt{3}$x+1=0有解的卡片概率.
解答 解:∵k+2≠0且△=(2$\sqrt{3}$)2-4(k+2)≥0,
∴k≤1且k≠-2,
∵2-1=1,5-1=4,0-1=-1,3-1=2,
∴从四张卡片中任取一张上写有数字2,0的满足条件,
∴抽到能使一元二次方程(k+2)x2-2$\sqrt{3}$x+1=0有解的卡片概率=$\frac{2}{4}$=$\frac{1}{2}$.
故答案为$\frac{1}{2}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义以及概率公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.可以用来说明命题“若|a|>0.5,则a>0.5”是假命题的反例( )
| A. | 可以是a=-1,也可以是 a=1 | B. | 可以是a=1,不可以是 a=-1 | ||
| C. | 可以是a=-1,不可以是 a=1 | D. | 既不可以是a=-1,也不可以是 a=1 |
8. 如图,在△ABC中,AB=8,点D、E分别是AB、AC的中点,BF平分∠ABC交DE于F,则DF的长是( )
如图,在△ABC中,AB=8,点D、E分别是AB、AC的中点,BF平分∠ABC交DE于F,则DF的长是( )
 如图,在△ABC中,AB=8,点D、E分别是AB、AC的中点,BF平分∠ABC交DE于F,则DF的长是( )
如图,在△ABC中,AB=8,点D、E分别是AB、AC的中点,BF平分∠ABC交DE于F,则DF的长是( )| A. | 2 | B. | 2.5 | C. | 3 | D. | 4 |
15.某同学进行社会调查,随机抽查了某个地区的20个家庭的收入情况,并绘制了统计图,请你根据统计图给出的信息回答:

(1)填写完成下表:
这20个家庭的年平均收入为1.6万元;
(2)样本中的中位数是1.2万元,众数是1.3万元;
(3)在平均数、中位数两数中,中位数更能反映这个地区家庭的年收入水平.

(1)填写完成下表:
| 年收入(万元) | 0.6 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 9.7 |
| 户 数 | 1 | 1 | 2 | 4 |
(2)样本中的中位数是1.2万元,众数是1.3万元;
(3)在平均数、中位数两数中,中位数更能反映这个地区家庭的年收入水平.
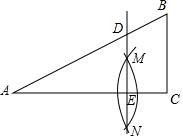 如图,在△ABC中,∠ACB=90°,以点A为圆心,以某一长度为半径画弧,再以点C为圆心,以另一长度为半径画弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E.求证:DE∥BC.
如图,在△ABC中,∠ACB=90°,以点A为圆心,以某一长度为半径画弧,再以点C为圆心,以另一长度为半径画弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E.求证:DE∥BC.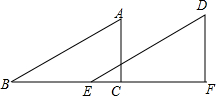 如图,把三角形△ABC沿直线BC的方向平移6cm得到三角形DEF,已知∠A=63°,∠B=27°,AC=4cm,BC=8cm,你能求出哪些角的度数?哪些边的长度?请直接写出结果.(至少写出5个结果)
如图,把三角形△ABC沿直线BC的方向平移6cm得到三角形DEF,已知∠A=63°,∠B=27°,AC=4cm,BC=8cm,你能求出哪些角的度数?哪些边的长度?请直接写出结果.(至少写出5个结果)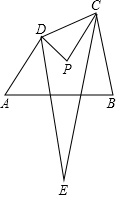 如图,在四边形ABCD中,∠C与∠D的平分线相交于点P,且∠A=60°,∠B=80°.
如图,在四边形ABCD中,∠C与∠D的平分线相交于点P,且∠A=60°,∠B=80°. 如图.已知△ABC中,△ADE∽△ABC,AD:BD=3:4,求S△ADE:S四边形DECB.
如图.已知△ABC中,△ADE∽△ABC,AD:BD=3:4,求S△ADE:S四边形DECB.