题目内容
10.在不同的直角坐标系中分别画出下列函数的图象:(1)y=3x+2
(2)y=-3x+2
(3)y=3x-2
(4)y=-3x-2.
分析 (1)根据一次函数图象上点的坐标特征求出直线与坐标轴的交点坐标,依此画出函数图象即可;
(2)根据一次函数图象上点的坐标特征求出直线与坐标轴的交点坐标,依此画出函数图象即可;
(3)根据一次函数图象上点的坐标特征求出直线与坐标轴的交点坐标,依此画出函数图象即可;
(4)根据一次函数图象上点的坐标特征求出直线与坐标轴的交点坐标,依此画出函数图象即可.
解答 解:(1)当x=0时,y=3x+2=2;
当y=3x+2=0时,x=-$\frac{2}{3}$.
∴直线y=3x+2过点(0,2)和(-$\frac{2}{3}$,0).
画出函数图象如图(1)所示.
(2)当x=0时,y=-3x+2=2;
当y=-3x+2=0时,y=$\frac{2}{3}$.
∴直线y=-3x+2过点(0,2)和($\frac{2}{3}$,0).
画出函数图象如图(2)所示.
(3)当x=0时,y=3x-2=-2;
当y=3x-2=0时,y=$\frac{2}{3}$.
∴直线y=3x-2过点(0,-2)和($\frac{2}{3}$,0).
画出函数图象如图(3)所示.
(4)当x=0时,y=-3x-2=-2;
当y=-3x-2=0时,y=-$\frac{2}{3}$.
∴直线y=-3x-2过点(0,-2)和(-$\frac{2}{3}$,0).
画出函数图象如图(4)所示.
点评 本题考查了一次函数的图象以及一次函数图象上点的坐标特征,根据一次函数图象上点的坐标特征找出直线与坐标轴的交点坐标是解题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
1.已知$\sqrt{a+2}$+(b-1)2=0,则(a+b)2016的值是( )
| A. | -1 | B. | 1 | C. | 2014 | D. | -2014 |
5. 如图,⊙O是四边形ABCD的外接圆,若∠O=110°,则∠C的度数为( )
如图,⊙O是四边形ABCD的外接圆,若∠O=110°,则∠C的度数为( )
 如图,⊙O是四边形ABCD的外接圆,若∠O=110°,则∠C的度数为( )
如图,⊙O是四边形ABCD的外接圆,若∠O=110°,则∠C的度数为( )| A. | 125° | B. | 120° | C. | 105° | D. | 90° |
19.-7的绝对值是( )
| A. | -7 | B. | 7 | C. | ±7 | D. | $\frac{1}{7}$ |
20.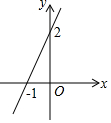 如图所示是一次函数y=kx+b在直角坐标系中的图象,通过观察图象我们就可以得到方程kx+b=0的解为x=-1,这一求解过程主要体现的数学思想是( )
如图所示是一次函数y=kx+b在直角坐标系中的图象,通过观察图象我们就可以得到方程kx+b=0的解为x=-1,这一求解过程主要体现的数学思想是( )
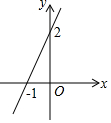 如图所示是一次函数y=kx+b在直角坐标系中的图象,通过观察图象我们就可以得到方程kx+b=0的解为x=-1,这一求解过程主要体现的数学思想是( )
如图所示是一次函数y=kx+b在直角坐标系中的图象,通过观察图象我们就可以得到方程kx+b=0的解为x=-1,这一求解过程主要体现的数学思想是( )| A. | 数形结合 | B. | 分类讨论 | C. | 类比 | D. | 公理化 |