题目内容
3.若0<x<1,则x、x2、$\sqrt{x}$中,最小的数是x2.分析 利用特殊值法进行判定.
解答 解:利用特殊值进行判定,
令x=$\frac{1}{4}$时,x2=($\frac{1}{4}$)2=$\frac{1}{16}$,$\sqrt{x}$=$\sqrt{\frac{1}{4}}$=$\frac{1}{2}$
∵$\frac{1}{2}$>$\frac{1}{4}$$>\frac{1}{16}$
∴最小的数是$\frac{1}{16}$,即最小的数是x2
故答案为:x2.
点评 本题考查了实数的大小比较,具体作法是:①正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小.②利用数轴比较任意两个实数的大小,即在数轴上表示的两个实数,右边的总比左边的大,在原点左侧,绝对值大的反而小.③对于同一字母的式子进行大小比较,可以利用代入特殊值法进行比较.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
11.205001精确到万位的近似数是( )
| A. | 20万 | B. | 21万 | C. | 2万 | D. | 2.05万 |
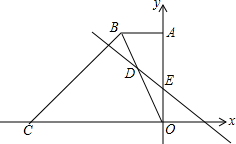 如图,在平面直角坐标系中,直角梯形OABC的边OC,OA分别与x轴,y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,BC=6$\sqrt{2}$,点C的坐标为(-9,0).
如图,在平面直角坐标系中,直角梯形OABC的边OC,OA分别与x轴,y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,BC=6$\sqrt{2}$,点C的坐标为(-9,0). 如图,在长方形ABCD中,边AB、BC的长(AB<BC)是方程x2-7x+12=0的两个根,点P从点A出发,以每秒1个单位的速度沿△ABC边A→B→C→A的方向运动,运动时间为t(秒).
如图,在长方形ABCD中,边AB、BC的长(AB<BC)是方程x2-7x+12=0的两个根,点P从点A出发,以每秒1个单位的速度沿△ABC边A→B→C→A的方向运动,运动时间为t(秒). 如图,要使得△ABC≌△DFE,已知∠A=∠D,AB=DF,根据AAS还需要的条件是∠ACB=∠DEF.
如图,要使得△ABC≌△DFE,已知∠A=∠D,AB=DF,根据AAS还需要的条件是∠ACB=∠DEF.