题目内容
10. 如图,OA⊥OB,OC⊥OD,OE是OD的反向延长线.
如图,OA⊥OB,OC⊥OD,OE是OD的反向延长线.(1)试说明:∠AOC=∠BOD;
(2)若∠BOD=32°,求∠AOE的度数.
分析 (1)根据余角的计算即可解题;
(2)根据余角的和为90°即可求得∠AOE的值.
解答 解:(1)∵OA⊥OB,OC⊥OD,
∴∠AOB=90°,∠COD=90°,
∵∠AOB=∠AOC+∠BOC=90°,∠COD=∠BOD+∠BOC=90°,
∴∠AOC=∠BOD;
(2)∵∠BOD=32°,
∴∠AOC=32°,
∴∠AOE=90°-32°=58°.
点评 本题考查了余角和为90°的性质,解决本题的关键是同角的余角相等.

练习册系列答案
相关题目
3. 如图,已知AB∥CD,BE平分∠ABC,且交CD于点D,∠CDE=150°,则∠C为( )
如图,已知AB∥CD,BE平分∠ABC,且交CD于点D,∠CDE=150°,则∠C为( )
 如图,已知AB∥CD,BE平分∠ABC,且交CD于点D,∠CDE=150°,则∠C为( )
如图,已知AB∥CD,BE平分∠ABC,且交CD于点D,∠CDE=150°,则∠C为( )| A. | 120° | B. | 150° | C. | 135° | D. | 110° |
19.点P是直线l外一点,点A、B、C是直线l上三点,且PA=10,PB=8,PC=6,那么点P到直线l的距离为( )
| A. | 6 | B. | 8 | C. | 不大于6的数 | D. | 小于6的数 |
19.某商品原价168元,经过连续两次降价后的售价为128元,设平均每次降价的百分数为x,则下面所列方程中正确的是( )
| A. | 168(1+x)2=128 | B. | 168(1-x)2=128 | C. | 168(1-2x)2=128 | D. | 168(1-x2)=128 |
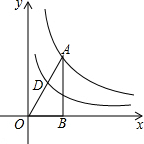 如图,反比例函数y=$\frac{2}{x}$的图象经过△ABO的顶点A,点D是OA的中点,若反比例函数y=$\frac{k}{x}$的图象经过点D,则k的值为$\frac{1}{2}$.
如图,反比例函数y=$\frac{2}{x}$的图象经过△ABO的顶点A,点D是OA的中点,若反比例函数y=$\frac{k}{x}$的图象经过点D,则k的值为$\frac{1}{2}$. 如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是(-2,0)或(2,10).
如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是(-2,0)或(2,10).