题目内容
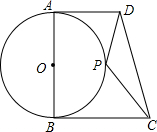 已知:AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=3,AB=4,BC=6,则△PCD的面积的最小值是( )
已知:AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=3,AB=4,BC=6,则△PCD的面积的最小值是( )| A、2 | B、4 | C、8 | D、9 |
考点:切线的性质
专题:
分析:由CD是固定的,所以当P到CD的距离最小时△PCD的面积最小,过P作EF∥CD,交AD于点E,交BC于点F,当EF与⊙O相切时,P到CD的距离最短,连接OP并延长交CD于点Q,过O作OH∥BC,交EF于点G,交CD于点H,则可知OH为梯形ABCD的中位线,OG为梯形ABFE的中位线,可求得OH,过D作DM⊥BC于点M,可求得CD=EF=5,由切线长定理可知AE=EP,BF=PF,可得AE+BF=EF=5,可求得OG=2.5,可求得GH=2,又OP=2,且
=
,可求得PQ=1.6,可求得△PCD的面积,可得出答案.
| OP |
| PQ |
| OG |
| GH |
解答:解:由CD是固定的,所以当P到CD的距离最小时△PCD的面积最小,
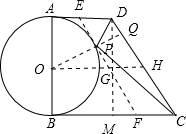 过P作EF∥CD,交AD于点E,交BC于点F,
过P作EF∥CD,交AD于点E,交BC于点F,
当EF与⊙O相切时,P到CD的距离最短,连接OP并延长交CD于点Q,
过O作OH∥BC,交EF于点G,交CD于点H,
则可知OH为梯形ABCD的中位线,OG为梯形ABFE的中位线,
∴OH=
(AD+BC)=4.5,
过D作DM⊥BC于点M,则DM=AB=4,MC=BC-AD=3,
∴CD=EF=5,
由切线长定理可知AE=EP,BF=PF,
∴AE+BF=EF=5,
∴OG=
(AE+BF)=2.5,
∴GH=OH-OG=4.5-2.5=2,
又∵OP=2,且
=
,
∴
=
,
∴PQ=1.6,
∴S△PCD=
PQ•CD=
×1.6×5=4,
故选B.
 过P作EF∥CD,交AD于点E,交BC于点F,
过P作EF∥CD,交AD于点E,交BC于点F,当EF与⊙O相切时,P到CD的距离最短,连接OP并延长交CD于点Q,
过O作OH∥BC,交EF于点G,交CD于点H,
则可知OH为梯形ABCD的中位线,OG为梯形ABFE的中位线,
∴OH=
| 1 |
| 2 |
过D作DM⊥BC于点M,则DM=AB=4,MC=BC-AD=3,
∴CD=EF=5,
由切线长定理可知AE=EP,BF=PF,
∴AE+BF=EF=5,
∴OG=
| 1 |
| 2 |
∴GH=OH-OG=4.5-2.5=2,
又∵OP=2,且
| OP |
| PQ |
| OG |
| GH |
∴
| 2 |
| PQ |
| 2.5 |
| 2 |
∴PQ=1.6,
∴S△PCD=
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题主要考查切线的性质及平行线分线段成比例、梯形的中位线等知识,确定出△PCD面积最小时的点P的位置是解题的关键.在求PQ的长时注意梯形中位线及线段成比例的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在直角坐标系中,以A(
如图,在直角坐标系中,以A( 如图,在⊙O中,AC为直径,点B、D在⊙O上,且AD=DC,DE⊥AB于E,四边形ABCD的面积是18,求DE的长.
如图,在⊙O中,AC为直径,点B、D在⊙O上,且AD=DC,DE⊥AB于E,四边形ABCD的面积是18,求DE的长. 如图,△ABC中,DE∥BC,DF∥AC,求证:△ADE∽△DBF.
如图,△ABC中,DE∥BC,DF∥AC,求证:△ADE∽△DBF.