题目内容
 如图,在⊙O中,AC为直径,点B、D在⊙O上,且AD=DC,DE⊥AB于E,四边形ABCD的面积是18,求DE的长.
如图,在⊙O中,AC为直径,点B、D在⊙O上,且AD=DC,DE⊥AB于E,四边形ABCD的面积是18,求DE的长.考点:全等三角形的判定与性质,正方形的判定与性质,圆周角定理
专题:
分析:把△ADE绕A点旋到△DCF处,使AD与CD重合,根据旋转的性质得到DF=DE,∠DCF=∠A,得到∠DCF+∠DCB=180°,即F、C、B三点共线,所以S四边形ABCD=S四边形DEBF,而四边形DEBF是正方形,得到DE2=8,得到DE的长.
解答:
解:把△ADE绕D点旋转到△DCF处,使AD与DC重合,
∴DF=AE,∠DCF=∠A,
∵∠ADC=∠ABC=90°
∴∠A+∠DCB=180°,
∴∠DCF+∠DCB=180°,
∴F、C、B三点共线,
∴S四边形ABCD=S四边形DEBF,
∵DE=DF,四个角都为90度,
∴四边形DEBF是正方形,
∴DE2=8,
∴DE=2
.

解:把△ADE绕D点旋转到△DCF处,使AD与DC重合,
∴DF=AE,∠DCF=∠A,
∵∠ADC=∠ABC=90°
∴∠A+∠DCB=180°,
∴∠DCF+∠DCB=180°,
∴F、C、B三点共线,
∴S四边形ABCD=S四边形DEBF,
∵DE=DF,四个角都为90度,
∴四边形DEBF是正方形,
∴DE2=8,
∴DE=2
| 2 |
点评:本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了正方形的性质.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么关于该班40名同学一周参加体育锻炼时间的说法错误的是( )
如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么关于该班40名同学一周参加体育锻炼时间的说法错误的是( )| A、中位数9 |
| B、平均数小于8.5 |
| C、众数是8 |
| D、锻炼时间超过8小时的有21人 |
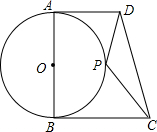 已知:AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=3,AB=4,BC=6,则△PCD的面积的最小值是( )
已知:AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=3,AB=4,BC=6,则△PCD的面积的最小值是( )