题目内容
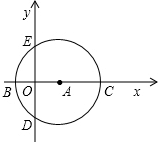 如图,在直角坐标系中,以A(
如图,在直角坐标系中,以A(| 3 |
| 3 |
(1)若抛物线y=
| 1 |
| 3 |
(2)判断点B是否在(1)中抛物线上,并画出(1)抛物线草图;
(3)设M为(1)中抛物线的对称轴上的一点,在第一象限内抛物线上是否存在这样点P,使得四边形CBMP是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
考点:圆的综合题
专题:
分析:(1)由条件可知AC=AB=2
,OA=BO=
,在Rt△AOD中可求得OD=OE=3,可得出C、D坐标,代入可求得b和c,可求得解析式;
(2)把B点坐标代入验证即可,再利用描点法画图;
(3)假设存在,设P点坐标为(t,s),当PM∥BC时,则PM=BC=4
,而PM=|t-
|可求得t的值,代入抛物线解析式可求得P点坐标,当BM∥PC时,则A为PM的中点,则P点只能在对称轴上,即P为抛物线的顶点.
| 3 |
| 3 |
(2)把B点坐标代入验证即可,再利用描点法画图;
(3)假设存在,设P点坐标为(t,s),当PM∥BC时,则PM=BC=4
| 3 |
| 3 |
解答:解:(1)如图1,连接AD,则AC=AD=AB=2
,

∵A(
,0),
∴AO=BO=
,
在Rt△OAD中,由勾股定理可求得OD=3,
且OC=3
,
∴C(3
,0),D(0,-3),
代入y=
x2+bx+c可求得c=-3,b=-
,
∴抛物线的解析式为:y=
x2-
x-3;
(2)由(1)可知B点坐标为(-
,0),满足y=
x2-
x-3,
∴B点在抛物线上,
由y=
x2-
x-3可知该二次函数开口向上,对称轴方程为x=
,与x轴的交点坐标为(-
,0)和(3
,0),与y轴的交点坐标为(0,-3),顶点坐标为(
,-4),
利用描点法可画出其函数图象,如图2;

(3)假设存在,设P点坐标为(t,s),
由(1)可求得BC=4
,
当PM∥BC时,则PM=BC=4
如图3,过P作PN⊥BC,交x轴于点N,

则AN=ON-OA=|t-
|,
又ON=PM=4
,即|t-
|=4
,解得t=5
或t=-3
,
代入y=
x2-
x-3可求得s=12,
∴P点坐标为(-3
,12)或(5
,12);
当BM∥PC时,则MP为对称线,必过BC的中点A,则P点在对称轴上,
∴P为二次函数的顶点,其坐标为(
,-4);
综上可知存在使得四边形CBMP是平行四边形的P点,其坐标为(-3
,12)或(5
,12)或(
,-4).
| 3 |

∵A(
| 3 |
∴AO=BO=
| 3 |
在Rt△OAD中,由勾股定理可求得OD=3,
且OC=3
| 3 |
∴C(3
| 3 |
代入y=
| 1 |
| 3 |
2
| ||
| 3 |
∴抛物线的解析式为:y=
| 1 |
| 3 |
2
| ||
| 3 |
(2)由(1)可知B点坐标为(-
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
∴B点在抛物线上,
由y=
| 1 |
| 3 |
2
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
利用描点法可画出其函数图象,如图2;

(3)假设存在,设P点坐标为(t,s),
由(1)可求得BC=4
| 3 |
当PM∥BC时,则PM=BC=4
| 3 |

则AN=ON-OA=|t-
| 3 |
又ON=PM=4
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
代入y=
| 1 |
| 3 |
2
| ||
| 3 |
∴P点坐标为(-3
| 3 |
| 3 |
当BM∥PC时,则MP为对称线,必过BC的中点A,则P点在对称轴上,
∴P为二次函数的顶点,其坐标为(
| 3 |
综上可知存在使得四边形CBMP是平行四边形的P点,其坐标为(-3
| 3 |
| 3 |
| 3 |
点评:本题主要考查待定系数法求二次函数解析式和垂径定理、平行四边形的性质等知识的综合应用,利用待定系数法求解析式时关键是求出点的坐标,在(3)中确定出点P可能出现的位置是解题的关键,注意方程思想的应用.

练习册系列答案
相关题目
 如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么关于该班40名同学一周参加体育锻炼时间的说法错误的是( )
如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么关于该班40名同学一周参加体育锻炼时间的说法错误的是( )| A、中位数9 |
| B、平均数小于8.5 |
| C、众数是8 |
| D、锻炼时间超过8小时的有21人 |
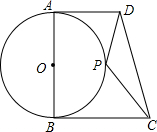 已知:AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=3,AB=4,BC=6,则△PCD的面积的最小值是( )
已知:AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=3,AB=4,BC=6,则△PCD的面积的最小值是( )