Question

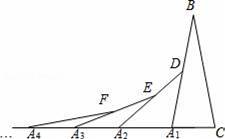
平面上，Rt△ABC与直径为CE的半圆O如图1摆放，∠B=90°，AC=2CE=m，BC=n，半圆O交BC边于点D，将半圆O绕点C按逆时针方向旋转，点D随半圆O旋转且∠ECD始终等于∠ACB，旋转角记为α（0°≤α≤180°）．

（1）①当α=0°时，连接DE，则∠CDE=　　　　　　°，CD=　　　　　　；②当α=180°时， =　　　　　　．

（2）试判断：旋转过程中的大小有无变化？请仅就图2的情形给出证明．

（3）若m=10，n=8，当α=∠ACB时，线段BD=　　　　　　．

（4）若m=6，n=，当半圆O旋转至与△ABC的边相切时，线段BD=　　　　　　．

　

Answer 1

【考点】圆的综合题．

【分析】（1）①根据直径的性质，由DE∥AB得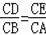即可解决问题．②求出BD、AE即可解决问题．

（2）只要证明△ACE∽△BCD即可．

（3）求出AB、AE，利用△ACE∽△BCD即可解决问题．

（4）分类讨论：①如图5中，当α=90°时，半圆与AC相切，②如图6中，当α=90°+∠ACB时，半圆与BC相切，分别求出BD即可．

【解答】（1）解：①如图1中

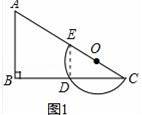
当α=0时，连接DE，则∠CDE=90°，

∵∠CDE=∠B=90°，

∴DE∥AB，

∴=，

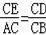
∵BC=n，

∴CD=．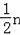

故答案为90°，n．

②如图2中，当α=180°时，BD=BC+CD=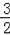n，AE=AC+CE=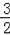m，

∴=．

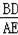
故答案为．

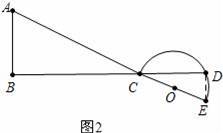
（2）如图3中，

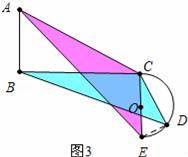
∵∠ACB=∠DCE，

∴∠ACE=∠BCD，

∵，

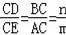
∴△ACE∽△BCD，

∴．

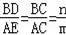
（3）如图4中，当α=∠ACB时，

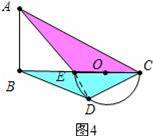
在RT△ABC中，∵AC=10，BC=8，∴AB=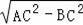=6，

在RT△ABE中．∵AB=6，BE=BC﹣CE=3，

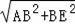
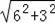
∴AE===3，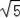

由（2）可知△ACE∽△BCD，

∴，

∴=，

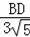
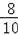
∴BD=，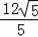

故答案为．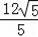

（4）∵m=6，n=，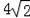

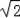
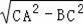
∴CE=3，CD=2，AB==2，

①如图5中，当α=90°时，半圆与AC相切，

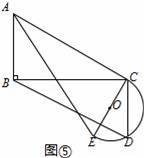
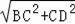
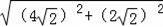
在RT△DBC中，BD===2．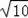

②如图6中，当α=90°+∠ACB时，半圆与BC相切，

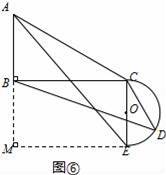
作EM⊥AB于M，

∵∠M=∠CBM=∠BCE=90°，

∴四边形BCEM是矩形，

∴，

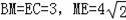
∴AM=5，AE==，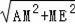

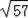
由（2）可知=，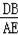

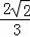
∴BD=．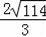

故答案为2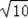或．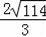

【点评】本题考查圆的有关知识，相似三角形的判定和性质、勾股定理等知识，正确画出图形是解决问题的关键，学会分类讨论的思想，本题综合性比较强，属于中考压轴题．