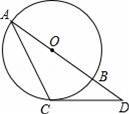
题目内容
如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（ ）
A．2
B．2
C．3 D．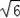
A【考点】轴对称-最短路线问题．
【专题】计算题；压轴题．
【分析】由于点B与D关于AC对称，所以连接BD，与AC的交点即为P点．此时PD+PE=BE最小，而BE是等边△ABE的边，BE=AB，由正方形ABCD的面积为12，可求出AB的长，从而得出结果．
【解答】解：设BE与AC交于点F（P′），连接BD，
∵点B与D关于AC对称，
∴P′D=P′B，
∴P′D+P′E=P′B+P′E=BE最小．
即P在AC与BE的交点上时，PD+PE最小，为BE的长度；
∵正方形ABCD的面积为12，
∴AB=2
．
又∵△ABE是等边三角形，
∴BE=AB=2
．
故所求最小值为2．
故选：A．
【点评】此题主要考查轴对称﹣﹣最短路线问题，要灵活运用对称性解决此类问题．
练习册系列答案
相关题目
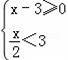
的所有整数解之和是（ ）
÷（
﹣
），再从﹣2＜x＜3的范围内选取一个你最喜欢的值代入，求值．
= ．
，当半圆O旋转至与△ABC的边相切时，线段BD= ．
是整数，则满足条件的最小正整数n为（ ）
