题目内容
1.若实数m,n满足$\sqrt{m+1}+(n-3)^{2}=0$,则m3+n0=0.分析 先根据非负数的性质求出m、n的值,再代入代数式进行计算即可.
解答 解:∵实数m,n满足$\sqrt{m+1}+(n-3)^{2}=0$,
∴m+1=0,n-3=0,
∴m=-1,n=3,
∴原式=(-1)3+30=-1+1=0.
故答案为:0.
点评 本题考查的是非负数的性质,熟知算术平方根具有非负性是解答此题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
13.函数y=$\sqrt{5+x}$中自变量x的取值范围是( )
| A. | x≥-5 | B. | x≥5 | C. | x>-5 | D. | x>5 |
 如图,管中放置着三根同样的绳子AA1、BB1、CC1.
如图,管中放置着三根同样的绳子AA1、BB1、CC1. 如图,MA,MB分别为⊙O的切线,A,B分别为切点,∠AMB=60°,点M到圆心O的距离OM=2,则⊙O的半径为1.
如图,MA,MB分别为⊙O的切线,A,B分别为切点,∠AMB=60°,点M到圆心O的距离OM=2,则⊙O的半径为1.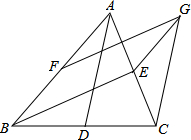 如图,在△ABC中,D、E、F为其三边中点.EG∥AB,FG∥BE,EG与FG交于点G,连接CG,求证:CG=AD.
如图,在△ABC中,D、E、F为其三边中点.EG∥AB,FG∥BE,EG与FG交于点G,连接CG,求证:CG=AD.