题目内容
12.已知等腰三角形的底边长为8,腰长a满足等式a(a-5)=4(a-5),求这个三角形的面积.分析 利用因式分解法解方程a(a-5)=4(a-5)得a1=5,a2=4,利用三角形三边的关系得a=5,即三角形三边分别为5,5,8,接着画出几何图形:如图,在△ABC中,CA=CB=5,AB=8,作CD⊥AB于D,根据等腰三角形的性质得AD=BD=4,则可根据勾股定理计算出CD=3,然后根据三角形面积公式求解.
解答 解:a(a-5)-4(a-5)=0,
(a-5)(a-4)=0,
所以a1=5,a2=4,
由于4+4=8,不满足三角形三边的关系,
所以a=5,
即三角形三边分别为5,5,8,
如图,在△ABC中,CA=CB=5,AB=8,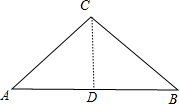 作CD⊥AB于D,则AD=BD=4,
作CD⊥AB于D,则AD=BD=4,
在Rt△ADB中,∵AD=4,AC=5,
∴CD=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴S△ABC=$\frac{1}{2}$×8×3=12.
答:这个三角形的面积为12.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了等腰三角形的性质和勾股定理.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
20.经过配方,方程x2-6x+7=0可以变形为( )
| A. | (x-3)2=16 | B. | (x+3)2=2 | C. | (x-6)2=29 | D. | (x-3)2=2 |
18.学校为了了解学生的身高情况,随机抽查了50名学生调查他们的身高,数据经整理制成不完整身高频数分布表:
根据以上信息,回答下列问题:
(1)a=13;
(2)身高范围在145≤x<155所占的百分比为20%,在155≤x<165范围内的人数最多;
(3)求这些学生身高的平均值;
(4)若该校有800名学生,求身高至少在165cm以上的学生人数.
| 身高(x/cm) | 人数(频数) |
| 145≤x<155 | 10 |
| 155≤x<165 | 25 |
| 165≤x<175 | a |
| 175≤x<185 | 2 |
(1)a=13;
(2)身高范围在145≤x<155所占的百分比为20%,在155≤x<165范围内的人数最多;
(3)求这些学生身高的平均值;
(4)若该校有800名学生,求身高至少在165cm以上的学生人数.
19.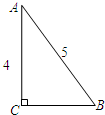 如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,以AC所在的直线为轴旋转一周,所得圆锥的侧面积为( )
如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,以AC所在的直线为轴旋转一周,所得圆锥的侧面积为( )
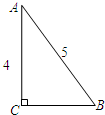 如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,以AC所在的直线为轴旋转一周,所得圆锥的侧面积为( )
如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,以AC所在的直线为轴旋转一周,所得圆锥的侧面积为( )| A. | 12π | B. | 15π | C. | 24π | D. | 30π |