题目内容
19.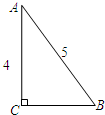 如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,以AC所在的直线为轴旋转一周,所得圆锥的侧面积为( )
如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,以AC所在的直线为轴旋转一周,所得圆锥的侧面积为( )| A. | 12π | B. | 15π | C. | 24π | D. | 30π |
分析 先利用勾股定理计算出BC=3,再判断以AC所在的直线为轴把△ABC旋转一周所得的几何体为圆锥,其底面圆的半径为3,母线长为5,然后利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.
解答 解:在Rt△ABC中,∵AB=5,AC=4,
∴BC=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵以AC所在的直线为轴把△ABC旋转一周所得的几何体为圆锥,其底面圆的半径为3,母线长为5,
∴这个圆锥的侧面积=$\frac{1}{2}$•2π•3•5=15π.
故选B.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
10.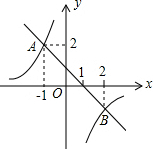 如图,直线y=-x+b与双曲线y=$\frac{k}{x}$交于点A,B,则不等式组$\frac{k}{x}$<-x+b<0的解集为( )
如图,直线y=-x+b与双曲线y=$\frac{k}{x}$交于点A,B,则不等式组$\frac{k}{x}$<-x+b<0的解集为( )
 如图,直线y=-x+b与双曲线y=$\frac{k}{x}$交于点A,B,则不等式组$\frac{k}{x}$<-x+b<0的解集为( )
如图,直线y=-x+b与双曲线y=$\frac{k}{x}$交于点A,B,则不等式组$\frac{k}{x}$<-x+b<0的解集为( )| A. | 0<x<2 | B. | x<-1或0<x<2 | C. | -1<x<2 | D. | 1<x<2 |
7.下列计算正确的是( )
| A. | (a2)3=a5 | B. | a6÷a6=0 | C. | (-2a)2=-4a2 | D. | a•a5=a6 |
14.当a>b时,下列不等式中正确的是( )
| A. | 2a<2b | B. | 2a+1<2b+1 | C. | a-3<b-3 | D. | -a<-b |
 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点.若青蛙从5这点开始跳,则经2013次跳后它停在的点所对应的数为( )
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点.若青蛙从5这点开始跳,则经2013次跳后它停在的点所对应的数为( )