题目内容
 完成下面的证明:
完成下面的证明:如图,已知△ABC,
求证:∠A+∠B+∠C=180°.
证明:延长BC到点D,过点C作CE∥AB,
∵CE∥AB,
∴∠A=∠
∵∠1+∠2+∠3═180°(
∴∠A+∠B+∠C=180°(
考点:三角形内角和定理,平行线的性质
专题:推理填空题
分析:延长BC到点D,过点C作CE∥AB,先根据平行线的性质得出∠A=∠1,∠B=∠2,再根据平角的定义即可得出结论.
解答:证明:延长BC,过点C作CE∥AB,
∵CE∥AB,
∴∠A=∠1,(两直线平所,内错角相等),∠B=∠2,(两直线平所,同位角相等),
∵∠1+∠2+∠3=180°(平角定义),
∴∠A+∠B+∠C=180°(等量代换).
故答案为:1,两直线平所,内错角相等,2,两直线平所,同位角相等,平角定义,等量代换.
∵CE∥AB,
∴∠A=∠1,(两直线平所,内错角相等),∠B=∠2,(两直线平所,同位角相等),
∵∠1+∠2+∠3=180°(平角定义),
∴∠A+∠B+∠C=180°(等量代换).
故答案为:1,两直线平所,内错角相等,2,两直线平所,同位角相等,平角定义,等量代换.
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
 如图,Rt△ABC中,AB=AC,BD平分∠ABC,DE⊥BC于E,AB=8cm,则DE+DC=
如图,Rt△ABC中,AB=AC,BD平分∠ABC,DE⊥BC于E,AB=8cm,则DE+DC=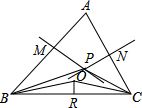 在不等边△ABC中,AB、AC的垂直平分线PM、PN交于点P,∠PBC、∠PCB的角平分线交与Q点,QR⊥BC于点R.求证:P、Q、R三点在同一直线上.
在不等边△ABC中,AB、AC的垂直平分线PM、PN交于点P,∠PBC、∠PCB的角平分线交与Q点,QR⊥BC于点R.求证:P、Q、R三点在同一直线上.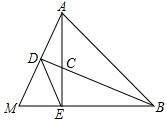 如图所示,AE、BD是△ABM的高,AE、BD交于点C,且AE=BE,BD平分∠ABM.
如图所示,AE、BD是△ABM的高,AE、BD交于点C,且AE=BE,BD平分∠ABM.
 平行四边形ABCD中,AC、BD交于O,E为AB上一点,EH∥AC,交BC于H,HO的延长线交AD于F.连接EF.求证:EF∥BD.
平行四边形ABCD中,AC、BD交于O,E为AB上一点,EH∥AC,交BC于H,HO的延长线交AD于F.连接EF.求证:EF∥BD.