题目内容
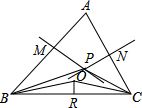 在不等边△ABC中,AB、AC的垂直平分线PM、PN交于点P,∠PBC、∠PCB的角平分线交与Q点,QR⊥BC于点R.求证:P、Q、R三点在同一直线上.
在不等边△ABC中,AB、AC的垂直平分线PM、PN交于点P,∠PBC、∠PCB的角平分线交与Q点,QR⊥BC于点R.求证:P、Q、R三点在同一直线上.考点:线段垂直平分线的性质
专题:证明题
分析:欲证明P、Q、R三点在同一直线上,只需证得直线PQ经过BC的中点R即可.
解答:证明:∵AB,AC的垂直平分线PM,PN交与点P,
∴点P是不等边△ABC的外接圆圆心,
∴PB=PC,
∴∠PBC=∠PCB,
∵∠PBC、∠PCB的平分线交与Q点,
∴∠QBR=
∠PBC,∠QCR=
∠PCB,
∴∠QBR=∠QCR,
∴QB=QC.
∵QR⊥BC,
∴RB=RC,
∴点P,Q,R在线段BC的垂直平分线上,即P、Q、R三点在同一直线上.
∴点P是不等边△ABC的外接圆圆心,
∴PB=PC,
∴∠PBC=∠PCB,
∵∠PBC、∠PCB的平分线交与Q点,
∴∠QBR=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠QBR=∠QCR,
∴QB=QC.
∵QR⊥BC,
∴RB=RC,
∴点P,Q,R在线段BC的垂直平分线上,即P、Q、R三点在同一直线上.
点评:本题考查了线段垂直平分线的性质.垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
相关题目
若不等式(3-m)x<2m-6的解集是x>-2,则m的取值范围是( )
| A、m<2 | B、m<3 |
| C、m>3 | D、m>4 |
 完成下面的证明:
完成下面的证明: