题目内容
已知OA、OB分别是两条射线,点C、D分别在OA、OB上.求作⊙P,使它与OA、OB、OC都相切.
考点:作图—复杂作图,切线的性质
专题:
分析:分别作∠O,∠ODC的角平分线,交于点P,再过P作PG⊥OA于点G,以P为圆心,PG为半径作圆即可.
解答:解:如图:①分别作∠O,∠ODC的角平分线,交于点P,
②过P作PG⊥OA于点G,
③以P为圆心,PG为半径作圆.

②过P作PG⊥OA于点G,
③以P为圆心,PG为半径作圆.

点评:本题主要考查了作图-复杂作图及切线的性质,解题的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
相关题目
若不等式(3-m)x<2m-6的解集是x>-2,则m的取值范围是( )
| A、m<2 | B、m<3 |
| C、m>3 | D、m>4 |
数轴上与坐标为3的点距离小于7的点的坐标x满足( )
| A、0<x-3<7 |
| B、-7<x-3<7 |
| C、-7≤x-3≤7 |
| D、x-3<7或x-3>7 |
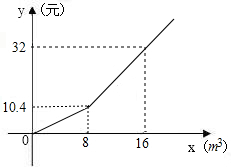 为了节约用水,某城市制定了两种如图用水标准,设某户每月用水量为xm3,应缴水费为y元,请你根据图象回答下列问题:
为了节约用水,某城市制定了两种如图用水标准,设某户每月用水量为xm3,应缴水费为y元,请你根据图象回答下列问题: 完成下面的证明:
完成下面的证明: 如图,△ABC中,D、E在BC上,且BD=CE,过AE上一点P作AB的平行线交AC于点M,交AD的延长线于点N,若PN=5PM,求DE:BC的值.
如图,△ABC中,D、E在BC上,且BD=CE,过AE上一点P作AB的平行线交AC于点M,交AD的延长线于点N,若PN=5PM,求DE:BC的值.