题目内容
平行四边形ABCD中，AC、BD交于O，E为AB上一点，EH∥AC，交BC于H，HO的延长线交AD于F．连接EF．求证：EF∥BD．考点：平行四边形的性质,全等三角形的判定与性质
专题：证明题
分析：由EH与AC平行，利用平行线等分线段定理列出关系式，根据ABCD为平行四边形，得到AD与BC平行，得到两对内错角相等，再由OA=OC，利用AAS得到三角形AOF与三角形COH全等，利用全等三角形对应边相等得到AF=CH，同理得到DF=BH，代入比例式即可得证．
解答：证明：∵EH∥AC，
∴
=
，
∵四边形ABCD为平行四边形，
∴AD∥BC，OA=OC，
∴∠OAF=∠OCH，∠AFO=∠CHO，
在△AOF和△COH中，
，
∴△AOF≌△COH（AAS），
∴AF=CH，
同理可得FD=BH，
∴
=
，
∴EF∥BD．
∴
| AE |
| EB |
| HC |
| HB |
∵四边形ABCD为平行四边形，
∴AD∥BC，OA=OC，
∴∠OAF=∠OCH，∠AFO=∠CHO，
在△AOF和△COH中，
|
∴△AOF≌△COH（AAS），
∴AF=CH，
同理可得FD=BH，
∴
| AE |
| EB |
| AF |
| FD |
∴EF∥BD．
点评：此题考查了平行四边形的性质，熟练掌握平行四边形的性质是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
完成下面的证明：
如图，△ABC中，D、E在BC上，且BD=CE，过AE上一点P作AB的平行线交AC于点M，交AD的延长线于点N，若PN=5PM，求DE：BC的值．
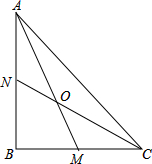如图，在Rt△ABC中，AB=BC=5，BN=BM=3，求△OBC面积．