题目内容
如图，Rt△ABC中，AB=AC，BD平分∠ABC，DE⊥BC于E，AB=8cm，则DE+DC=考点：角平分线的性质,等腰直角三角形
专题：
分析：根据角平分线上的点到角的两边距离相等可得AD=DE，然后求出DE+DC=AC．
解答：解：∵BD平分∠ABC，DE⊥BC，∠A=90°，
∴AD=DE，
∴DE+DC=AC，
∵AB=AC，AB=8cm，
∴DE+DC=8cm．
故答案为：8cm．
∴AD=DE，
∴DE+DC=AC，
∵AB=AC，AB=8cm，
∴DE+DC=8cm．
故答案为：8cm．
点评：本题考查了角平分线上的点到角的两边距离相等的性质，熟记性质是解题的关键．
练习册系列答案
相关题目
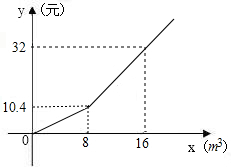为了节约用水，某城市制定了两种如图用水标准，设某户每月用水量为xm3，应缴水费为y元，请你根据图象回答下列问题：若不等式（3-m）x＜2m-6的解集是x＞-2，则m的取值范围是（ ）
| A、m＜2 | B、m＜3 |
| C、m＞3 | D、m＞4 |
完成下面的证明：