题目内容
如图1,在平面直角坐标系中,抛物线y=ax2+bx-2交x轴于A、B两点,交y轴于点C,且A(-1,0)、B(3,0).
(1)求该抛物线的表达式及顶点D的坐标;
(2)若点M是x轴上的一个动点,设△MDC的面积为S,动点M的坐标为(1,0),令Q=S(3t-19),当1<t<3时,Q是否有最小值?若有,请求出Q的最小值和此时t的值;若没有,请说明理由;
(3)在抛物线上有一个动点P,y轴上有一个动点N,使得以A、B、P、N为顶点的四边形是平行四边形,请求出点P的坐标.

(1)求该抛物线的表达式及顶点D的坐标;
(2)若点M是x轴上的一个动点,设△MDC的面积为S,动点M的坐标为(1,0),令Q=S(3t-19),当1<t<3时,Q是否有最小值?若有,请求出Q的最小值和此时t的值;若没有,请说明理由;
(3)在抛物线上有一个动点P,y轴上有一个动点N,使得以A、B、P、N为顶点的四边形是平行四边形,请求出点P的坐标.

考点:二次函数综合题
专题:
分析:(1)应用待定系数法把A、B点的坐标代入抛物线y=ax2+bx-2中即可解得,然后用求顶点的公式即可求得顶点坐标.
(2)用梯形的面积减去三角形的面积即可求得.
(3)依据平行四边形的性质即可设出P的坐标为(4,n),代入抛物线的解析式即可求得.
(2)用梯形的面积减去三角形的面积即可求得.
(3)依据平行四边形的性质即可设出P的坐标为(4,n),代入抛物线的解析式即可求得.
解答:(1)把A、B点的坐标代入抛物线y=ax2+bx-2的解析式得:
,
解得;
,
∴该抛物线的表达式为:y=
x2-
x-2,
∵y=
x2-
x-2,
∴y=
(x-1)2-
,
∴顶点D的坐标为:(1,-
).

(2)如图2所示,∵M(1,0),D(1,-
)、C(0,-2),
∴OM=1,OC=2,DM=
,
∴S△MCD=S梯形OCDM-S△OCM=
,
令Q=S(3t-19),
∴Q=
(3t-19)=4t-
,
∴当1<t<3时,Q是没有最小值.
(3)如图3所示,由A(-1,0)、B(3,0);
可知AB=4,
∵A、B、P、N为顶点的四边形是平行四边形;
∴设P点的坐标为(4,n),
把P点的坐标代入抛物线的表达式y=
x2-
x-2,
解得;n=
,
∴P点的坐标为:(4,
).
|
解得;
|
∴该抛物线的表达式为:y=
| 2 |
| 3 |
| 4 |
| 3 |
∵y=
| 2 |
| 3 |
| 4 |
| 3 |
∴y=
| 2 |
| 3 |
| 8 |
| 3 |
∴顶点D的坐标为:(1,-
| 8 |
| 3 |

(2)如图2所示,∵M(1,0),D(1,-
| 8 |
| 3 |
∴OM=1,OC=2,DM=
| 8 |
| 3 |
∴S△MCD=S梯形OCDM-S△OCM=
| 4 |
| 3 |
令Q=S(3t-19),
∴Q=
| 4 |
| 3 |
| 76 |
| 3 |
∴当1<t<3时,Q是没有最小值.
(3)如图3所示,由A(-1,0)、B(3,0);
可知AB=4,
∵A、B、P、N为顶点的四边形是平行四边形;
∴设P点的坐标为(4,n),
把P点的坐标代入抛物线的表达式y=
| 2 |
| 3 |
| 4 |
| 3 |
解得;n=
| 10 |
| 3 |
∴P点的坐标为:(4,
| 10 |
| 3 |
点评:题主要考查对用待定系数法求二次函数的解析式,平行四边形的性质以及坐标系中面积的求法.

练习册系列答案
相关题目
若(x-3)0-2(3x-6)0有意义,则x的取值范围是( )
| A、x>3 |
| B、x>2 |
| C、x≠3或x≠2 |
| D、x≠3且x≠2 |
 如图,已知∠1+∠2=180°,∠DAE=∠BCF.
如图,已知∠1+∠2=180°,∠DAE=∠BCF.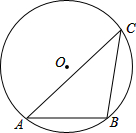 如图,圆O内接三角形△ABC.把△ABC以点O为旋转中心,顺时针方向旋转∠BOA的度数得到△EAF.
如图,圆O内接三角形△ABC.把△ABC以点O为旋转中心,顺时针方向旋转∠BOA的度数得到△EAF.