题目内容
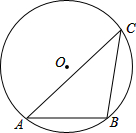 如图,圆O内接三角形△ABC.把△ABC以点O为旋转中心,顺时针方向旋转∠BOA的度数得到△EAF.
如图,圆O内接三角形△ABC.把△ABC以点O为旋转中心,顺时针方向旋转∠BOA的度数得到△EAF.(1)利用尺规作出△EAF(要求保留作图痕迹,不写作法)
(2)连接CE,设EF与AC,BC分别交于点K和D,求证:CD2=DE•DK.
考点:作图-旋转变换,相似三角形的判定与性质
专题:作图题,证明题
分析:(1)根据旋转的性质,点B旋转后与点A重合,再以点A为圆心,以AB为半径画弧,在点A的左侧与圆相交于点E,以BC为半径画弧,在点A的右侧与圆相交于点F,然后顺次连接即可;
(2)由作图可知∠AOB=∠AOE=∠COF,然后求出∠ACB=∠CEF,再判断出△CED和△KCD相似,根据相似三角形对应边成比例列式整理即可得证.
(2)由作图可知∠AOB=∠AOE=∠COF,然后求出∠ACB=∠CEF,再判断出△CED和△KCD相似,根据相似三角形对应边成比例列式整理即可得证.
解答: (1)解:△EAF如图所示;
(1)解:△EAF如图所示;
(2)证明:由(1)作图可知∠AOB=∠AOE=∠COF,
∴∠ACB=∠CEF,
又∵∠CDE=∠KDC,
∴△CED∽△KCD,
∴
=
,
即CD2=DE•DK.
 (1)解:△EAF如图所示;
(1)解:△EAF如图所示;(2)证明:由(1)作图可知∠AOB=∠AOE=∠COF,
∴∠ACB=∠CEF,
又∵∠CDE=∠KDC,
∴△CED∽△KCD,
∴
| CD |
| DE |
| DK |
| CD |
即CD2=DE•DK.
点评:本题考查了利用旋转变换作图,相似三角形的判定与性质,熟记旋转的性质并判断出旋转后点B与点A重合是解题的关键.

练习册系列答案
相关题目
若
在实数范围内有意义,则m的取值范围是( )
| 3m-6 |
| A、m≥0 | B、m≥-2 |
| C、m≥2 | D、m<2 |

 (以下两个题注明根据)
(以下两个题注明根据)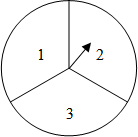 如图,一个可以自由转动的转盘被等分成3个扇形区域,上面分别标有数字1、2、3.甲、乙两位同学用该转盘做游戏.
如图,一个可以自由转动的转盘被等分成3个扇形区域,上面分别标有数字1、2、3.甲、乙两位同学用该转盘做游戏.