题目内容
18．已知（a+b）2=8，（a-b）2=5，则a2+b2=6.5，ab=0.75．分析 已知两式利用完全平方公式化简，相加减即可求出所求式子的值．
解答 解：∵（a+b）2=a2+2ab+b2=8①，（a-b）2=a2-2ab+b2=5②，
∴①+②得：2（a2+b2）=13，①-②得：4ab=3，
解得：a2+b2=6.5，ab=0.75，
故答案为：6.5；0.75
点评 此题考查了完全平方公式，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
相关题目
如图，三个正方形恰好围成一个直角三角形，它们的面积如图所示，则正方形A的面积为36．
13．下列统计中，适宜全面调查的是（ ）
| A． | 检测某城市的空气质量 | B． | 调查全国初中生的视力情况 | ||
| C． | 审查某篇文章的错别字 | D． | 调查某池塘中现有鱼的数量 |
已知实数a，b在数轴上的对应点如图所示，那么化简$\sqrt{（a-b）^{2}}$-$\sqrt{{a}^{2}}$=b．
7．如图1，将边长为1的正方形ABCD压扁为边长为1的菱形ABCD．在菱形ABCD中，∠A的大小为α，面积记为S．
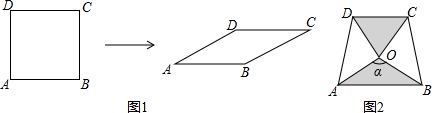
（1）请补全表：
（2）填空：
由（1）可以发现单位正方形在压扁的过程中，菱形的面积随着∠A大小的变化而变化，不妨把单位菱形的面积S记为S（α）．例如：当α=30°时，S=S（30°）=$\frac{1}{2}$；当α=135°时，S=S（135°）=$\frac{{\sqrt{2}}}{2}$．由上表可以得到S（60°）=S（120°）；S（150°）=S（30°），…，由此可以归纳出S（180°-α）=（α°）．
（3）两块相同的等腰直角三角板按图2的方式放置，AD=$\sqrt{2}$，∠AOB=α，试探究图中两个带阴影的三角形面积是否相等，并说明理由（注：可以利用（2）中的结论）．
（1）请补全表：
| α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
| S | $\frac{1}{2}$ | 1 | $\frac{{\sqrt{2}}}{2}$ |
由（1）可以发现单位正方形在压扁的过程中，菱形的面积随着∠A大小的变化而变化，不妨把单位菱形的面积S记为S（α）．例如：当α=30°时，S=S（30°）=$\frac{1}{2}$；当α=135°时，S=S（135°）=$\frac{{\sqrt{2}}}{2}$．由上表可以得到S（60°）=S（120°）；S（150°）=S（30°），…，由此可以归纳出S（180°-α）=（α°）．
（3）两块相同的等腰直角三角板按图2的方式放置，AD=$\sqrt{2}$，∠AOB=α，试探究图中两个带阴影的三角形面积是否相等，并说明理由（注：可以利用（2）中的结论）．