题目内容
9．若二次函数y=x2+2x+c的最小值是7，则它的图象与y轴的交点坐标是（0，8）．分析 根据二次函数最大（小）值的求法，利用公式法直接求得c的值，即可求得图象与y轴的交点坐标．
解答 解：∵二次函数y=x2+2x+c的最小值是7，
∴$\frac{4ac-{b}^{2}}{4a}$=$\frac{4c-4}{4}$=7，
解得c=8，
∴图象与y轴的交点坐标是（0，8），
故答案为（0，8）．
点评 本题考查了二次函数的最值，求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法．
练习册系列答案
相关题目
如图，一枚运载火箭从地面L处发射，当火箭到达A点时，从位于距发射架底部4km处的地面雷达站R（LR=4）测得火箭底部的仰角为43°．1s后，火箭到达B点，此时测得火箭底部的仰角为45.72°．这枚火箭从A到B的平均速度是多少 （结果取小数点后两位）？
20．校运动会上甲、乙、丙、丁四名选手参加100米决赛，赛场有1、2、3、4条跑道．如果选手以随机抽签的方式决定各自的跑道，则甲抽到1号跑道，乙抽到2号跑道的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{12}$ | D． | $\frac{1}{24}$ |
17．下列方程中是一元一次方程的是（ ）
| A． | x+3=3-x | B． | x+3=y+2 | C． | $\frac{1}{x}$=1 | D． | x2-1=0 |
4．一元二次方程x=x（x-2）的根是（ ）
| A． | 0或2 | B． | 0或3 | C． | 1或2 | D． | 3 |
如图，等边△ABC周长是12，AD是∠BAC的平分线，则BD=2．
已知数轴的原点为O，如图所示，点A表示-2，点B表示3，请回答下列问题：
19．
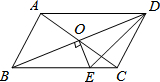如图，?ABCD的对角线相交于点O，且AB≠AD，过点O作OE⊥BD交BC于点E．若△CDE的周长为8cm，则?ABCD的周长为（ ）
如图，?ABCD的对角线相交于点O，且AB≠AD，过点O作OE⊥BD交BC于点E．若△CDE的周长为8cm，则?ABCD的周长为（ ）| A． | 8cm | B． | 12cm | C． | 16cm | D． | 24cm |