题目内容
18.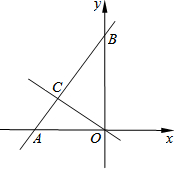 如图,一次函数y=mx+2m+3的图象与y=-$\frac{1}{2}$x的图象交于点C,且点C的横坐标为-3,与x轴、y轴分别交于点A、点B.
如图,一次函数y=mx+2m+3的图象与y=-$\frac{1}{2}$x的图象交于点C,且点C的横坐标为-3,与x轴、y轴分别交于点A、点B.(1)求m的值与AB的长;
(2)若点Q为线段OB上一点,且 S△OCQ=$\frac{1}{4}$S△BAO,求点Q的坐标.
分析 (1)把点C的横坐标代入正比例函数解析式,求得点C的纵坐标,然后把点C的坐标代入一次函数解析式即可求得m的值,从而得到一次函数的解析式,则易求点A、B的坐标,然后根据勾股定理即可求得AB;
(2)由S△OCQ=$\frac{1}{4}$S△BAO得到OQ的长,即可求得Q点的坐标.
解答 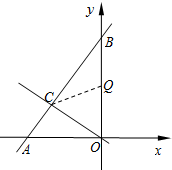 解:(1)∵点C在直线$y=-\frac{1}{2}x$上,点C的横坐标为-3,
解:(1)∵点C在直线$y=-\frac{1}{2}x$上,点C的横坐标为-3,
∴点C坐标为(-3,$\frac{3}{2}$),
又∵点C在直线y=mx+2m+3上,
∴$-3m+2m+3=\frac{3}{2}$,
∴$m=\frac{3}{2}$,
∴直线AB的函数表达式为$y=\frac{3}{2}x+6$,
令x=0,则y=6,令y=0,则$\frac{3}{2}$x+6=0,解得x=-4,
∴A(-4,0)、B(0,6),
∴AB=$\sqrt{{4}^{2}+{6}^{2}}$=$2\sqrt{13}$;
(2)∵${S_{△COQ}}=\frac{1}{4}{S_{△BAO}}$,
∴$\frac{3•OQ}{2}=\frac{1}{4}×\frac{4×6}{2}$,
∴OQ=2,
∴点Q坐标为(0,2).
点评 本题考查了两直线相交或平行问题、待定系数法求函数解析式、一次函数图象上点的坐标特征、勾股定理的应用、三角形的面积公式等知识,综合性较强,值得关注.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
8.若一个扇形的半径是18cm,且它的弧长是12π cm,则此扇形的圆心角等于( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
9.有这样一个问题:探究函数y=$\frac{1}{x-1}$+x的图象与性质.
小东根据学习函数的经验,对函数y=$\frac{1}{x-1}$+x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=$\frac{1}{x-1}$+x的自变量x的取值范围是x≠1;
(2)下表是y与x的几组对应值.
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可):该函数没有最大值,也没有最小值.
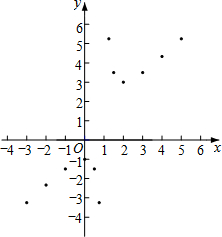
小东根据学习函数的经验,对函数y=$\frac{1}{x-1}$+x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=$\frac{1}{x-1}$+x的自变量x的取值范围是x≠1;
(2)下表是y与x的几组对应值.
| x | … | -3 | -2 | -1 | 0 | $\frac{1}{2}$ | $\frac{3}{4}$ | $\frac{5}{4}$ | $\frac{3}{2}$ | 2 | 3 | 4 | 5 | … |
| y | … | -$\frac{13}{4}$ | -$\frac{7}{3}$ | -$\frac{3}{2}$ | -1 | -$\frac{3}{2}$ | -$\frac{13}{4}$ | $\frac{21}{4}$ | $\frac{7}{2}$ | 3 | $\frac{7}{2}$ | m | $\frac{21}{4}$ | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可):该函数没有最大值,也没有最小值.
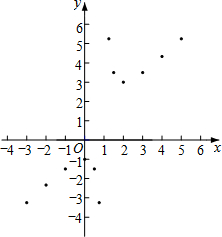
6.下列各数:π,$\frac{4}{3}$,0,-1中,无理数是( )
| A. | π | B. | $\frac{4}{3}$ | C. | 0 | D. | -1 |
7. 要用一根铁丝弯成如图所示的铁框,则这根铁丝至少长( )米?
要用一根铁丝弯成如图所示的铁框,则这根铁丝至少长( )米?
 要用一根铁丝弯成如图所示的铁框,则这根铁丝至少长( )米?
要用一根铁丝弯成如图所示的铁框,则这根铁丝至少长( )米?| A. | 2.5m | B. | 5m | C. | 4m | D. | 无法确定 |
 如图,小马虎设计了某个产品的包装盒,由于粗心少设计了其中的一部分,请你帮他补上,使该图形能折成一个密封的正方形盒子.
如图,小马虎设计了某个产品的包装盒,由于粗心少设计了其中的一部分,请你帮他补上,使该图形能折成一个密封的正方形盒子.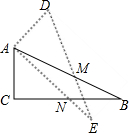 如图,在Rt△ABC中,∠C=90°,M为AB边上中点,将Rt△ABC绕点M旋转,使点C与点A重合得Rt△DEA,设AE交CB于点N.
如图,在Rt△ABC中,∠C=90°,M为AB边上中点,将Rt△ABC绕点M旋转,使点C与点A重合得Rt△DEA,设AE交CB于点N.