题目内容
13.如图,已知数轴上点A表示的数为7,点B表示的数为-5,点P从点A出发,沿数轴以每秒3个单位长度的速度向左匀速运动,同时,另一点Q从原点O出发,也沿数轴以每秒1个单位长度的速度向左匀速运动,设运动时间为t秒(t>0).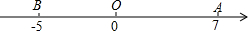
(1)线段AB的长度为12,数轴上点P和点Q表示的数分别为7-3t、-t(用含t的代数式表示);
(2)在点P和点Q的运动过程中,经过多少秒点P追上点Q?经过多少秒点B恰为PQ的中点?
(3)运动过程中,若时间t总满足|t+7|-|5-t|=12,则t的范围是t≥5.
分析 (1)根据点A、B表示的数利用两点间的距离公式即可求出线段AB的长度,再根据点P、Q运动的方向及速度即可找出点P、Q表示的数;
(2)当点P追上点Q时,结合点P、Q表示的数相等即可得出关于t的一元一次方程,解之即可得出结论;当点B恰为PQ的中点时,结合点P、B、Q表示的数之间的关系即可得出关于t的一元一次方程,解之即可得出结论;
(3)分t≤-7、-7<t≤5以及t>5三种情况去绝对值,由此即可得出结论.
解答 解:(1)线段AB的长度为7-(-5)=12,
当运动时间为t秒时,点P表示的数为7-3t,点Q表示的数为-t.
故答案为:12;7-3t;-t.
(2)当点P追上点Q时,有7-3t=-t,
解得:t=$\frac{7}{2}$;
当点B恰为PQ的中点时,有2×(-5)=7-3t+(-t),
解得:t=$\frac{17}{4}$.
(3)当t≤-7时,|t+7|-|5-t|=-t-7-5+t=-12,
∵-12≠-12,
∴t≤-7不合适;
当-7<t≤5时,|t+7|-|5-t|=t+7-5+t=2t+2=12,
解得:t=5.
当t>5时,|t+7|-|5-t|=t+7-t+5=12,
∵12=12,
∴t>5.
综上所述:t的范围是t≥5.
故答案为:t≥5.
点评 本题考查了一元一次方程的应用、绝对值以及整式的加减,根据数量关系找出关于t的一元一次方程是解题的关键.

练习册系列答案
相关题目
3.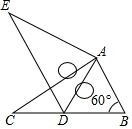 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为( )
 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为( )| A. | 0.5 | B. | 1.5 | C. | $\sqrt{2}$ | D. | 1 |
1.已知m、n是方程x2+3x-2=0的两个实数根,则m2+4m+n+2mn的值为( )
| A. | 1 | B. | 3 | C. | -5 | D. | -9 |
5.如果水位升高6m时水位变化记为+6m,那么水位下降6m时水位变化记为( )
| A. | -3 m | B. | 3 m | C. | 6 m | D. | -6 m |
