题目内容
从-3,-1,0,1,3这五个数中,任取两个不同的数分别作为m,n的值,恰好使得关于x,y的二元一次方程组
有整数解,且点(m,n)落在双曲线y=-
上的概率为 .
|
| 3 |
| x |
考点:列表法与树状图法,二元一次方程组的解,反比例函数图象上点的坐标特征
专题:
分析:首先用列表法或树形图得到所用可能的情况,若使点(m,n)落在双曲线y=-
上,则mn=-3,由此得到mn的关系式,再根据恰好使得关于x,y的二元一次方程组
有整数解,即可求出m,n的值,由此可得到点(m,n)落在双曲线y=-
上的概率.
| 3 |
| x |
|
| 3 |
| x |
解答:解:画树状图得:

若使点(m,n)落在双曲线y=-
上,则mn=-3,
∴点(m,n)可以是(1,-3)、(3,-1)、(-3,1)、(-1,3),
∵恰好使得关于x,y的二元一次方程组
有整数解,
∴点(m,n)可以是(1,-3)、(-3,1),
∴且点(m,n)落在双曲线y=-
上的概率为
=
,
故答案为:
.

若使点(m,n)落在双曲线y=-
| 3 |
| x |
∴点(m,n)可以是(1,-3)、(3,-1)、(-3,1)、(-1,3),
∵恰好使得关于x,y的二元一次方程组
|
∴点(m,n)可以是(1,-3)、(-3,1),
∴且点(m,n)落在双曲线y=-
| 3 |
| x |
| 2 |
| 20 |
| 1 |
| 10 |
故答案为:
| 1 |
| 10 |
点评:此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
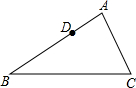 如图,在△ABC中,AB=4,AC=3,D、E分别是AB、AC上的动点,在边AC上取一点E,使A、D、E三点组成的三角形与△ABC相似.
如图,在△ABC中,AB=4,AC=3,D、E分别是AB、AC上的动点,在边AC上取一点E,使A、D、E三点组成的三角形与△ABC相似.
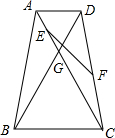 如图,梯形ABCD中,AD∥BC,AB=DC,AC交BD于G,且cos∠BGC=
如图,梯形ABCD中,AD∥BC,AB=DC,AC交BD于G,且cos∠BGC=