题目内容
20.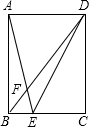 如图,在矩形ABCD中,AB=12,AD=9,点E是边BC上一点,连接AE,BD相交于点F,连接DE,若sin∠DEC=$\frac{2\sqrt{5}}{5}$,则BF=$\frac{15}{4}$.
如图,在矩形ABCD中,AB=12,AD=9,点E是边BC上一点,连接AE,BD相交于点F,连接DE,若sin∠DEC=$\frac{2\sqrt{5}}{5}$,则BF=$\frac{15}{4}$.
分析 由四边形ABCD是矩形,得到CD=AB=12,BC=AD=9,∠C=90°,根据勾股定理求得BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=15,根据sin∠DEC=$\frac{2\sqrt{5}}{5}$,得到DE=6$\sqrt{5}$,由勾股定理得到CE=$\sqrt{D{E}^{2}-C{D}^{2}}$=6,通过△ADF∽△EBF,即可得到结果.
解答 解:∵四边形ABCD是矩形,
∴CD=AB=12,BC=AD=9,∠C=90°,
∴BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=15,
∵sin∠DEC=$\frac{2\sqrt{5}}{5}$,
∴DE=6$\sqrt{5}$,
∴CE=$\sqrt{D{E}^{2}-C{D}^{2}}$=6,
∴BE=3,
∵AB∥BC,
∴△ADF∽△EBF,
∴$\frac{AD}{BE}=\frac{DF}{BF}$=$\frac{9}{3}$=3,
∴BF=$\frac{1}{4}$BD=$\frac{15}{4}$.
故答案为:$\frac{15}{4}$.
点评 此题考查了相似三角形的判定与性质,矩形的性质,勾股定理,熟练定理是解题的关键.

练习册系列答案
相关题目
11.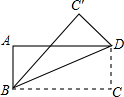 将矩形ABCD沿对角线BD折叠,使得C与C′重合,若DC′=2,则AB=( )
将矩形ABCD沿对角线BD折叠,使得C与C′重合,若DC′=2,则AB=( )
 将矩形ABCD沿对角线BD折叠,使得C与C′重合,若DC′=2,则AB=( )
将矩形ABCD沿对角线BD折叠,使得C与C′重合,若DC′=2,则AB=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.八(2)班组织了一次环保知识竞赛,甲乙两队各5人的成绩如下表所示(10分制).
(1)指出甲队成绩的中位数;
(2)指出乙队成绩的众数;
(3)若计算出方差为:S${\;}_{甲}^{2}$=1.84,S${\;}_{乙}^{2}$=1.04,判断哪队的成绩更整齐?
| 甲 | 9 | 8 | 10 | 6 | 9 |
| 乙 | 8 | 7 | 8 | 9 | 10 |
(2)指出乙队成绩的众数;
(3)若计算出方差为:S${\;}_{甲}^{2}$=1.84,S${\;}_{乙}^{2}$=1.04,判断哪队的成绩更整齐?
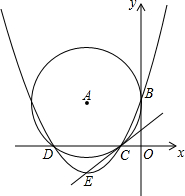 如图,在平面直角坐标系中,⊙A与x轴相交于C(-2,0),D(-8,0)两点,与y轴相切于点B(0,4).
如图,在平面直角坐标系中,⊙A与x轴相交于C(-2,0),D(-8,0)两点,与y轴相切于点B(0,4).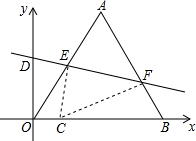 在平面直角坐标系中,等边三角形OAB的边长是2$\sqrt{3}$,且OB边落在x轴的正半轴上,点A落在第一象限.将△OAB沿直线y=kx+b折叠,使点A落在x轴上,设点C是点A落在x轴上的对应点.
在平面直角坐标系中,等边三角形OAB的边长是2$\sqrt{3}$,且OB边落在x轴的正半轴上,点A落在第一象限.将△OAB沿直线y=kx+b折叠,使点A落在x轴上,设点C是点A落在x轴上的对应点.  如图,在△ABC中,BC=6,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q.当CQ=$\frac{1}{2}$CE时,EP+BP=6;当CQ=$\frac{1}{n}$CE时,EP+BP=6n-6.(用含n的代数式表示)
如图,在△ABC中,BC=6,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q.当CQ=$\frac{1}{2}$CE时,EP+BP=6;当CQ=$\frac{1}{n}$CE时,EP+BP=6n-6.(用含n的代数式表示)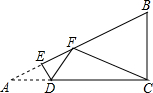 如图,有一直角三角形纸片ACB,∠A=30°,∠ACB=90°,BC=2,点D是AC边上一动点.过点D沿直线DE方向折叠三角形纸片,使点A落在射线AB上的点F处,当以点F、B、C为顶点的三角形为等腰三角形时,AD的长为$\frac{2\sqrt{3}}{3}$.
如图,有一直角三角形纸片ACB,∠A=30°,∠ACB=90°,BC=2,点D是AC边上一动点.过点D沿直线DE方向折叠三角形纸片,使点A落在射线AB上的点F处,当以点F、B、C为顶点的三角形为等腰三角形时,AD的长为$\frac{2\sqrt{3}}{3}$.