题目内容
11．
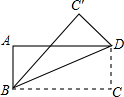将矩形ABCD沿对角线BD折叠，使得C与C′重合，若DC′=2，则AB=（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 根据矩形的对边相等可得CD=AB，再根据翻折变换的性质可得C′D=CD，代入数据即可得解．
解答 解：在矩形ABCD中，CD=AB，
∵矩形ABCD沿对角线BD折叠后点C和点C′重合，
∴C′D=CD，
∴C′D=AB，
∵DC′=2，
∴AB=2．
故选：B．
点评 本题考查了矩形的对边相等的性质，翻折变换的性质，是基础题，熟记性质是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
20．下列各数中，绝对值最大的数是（ ）
| A． | 5 | B． | -3 | C． | 0 | D． | -2 |
6．
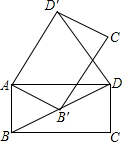如图，在矩形ABCD中，AB=1，BC=$\sqrt{3}$．将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′，使得点B′恰好落在对角线BD上，连接DD′，则DD′的长度为（ ）
如图，在矩形ABCD中，AB=1，BC=$\sqrt{3}$．将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′，使得点B′恰好落在对角线BD上，连接DD′，则DD′的长度为（ ）| A． | $\sqrt{3}$ | B． | $\sqrt{5}$ | C． | $\sqrt{3}$+1 | D． | 2 |
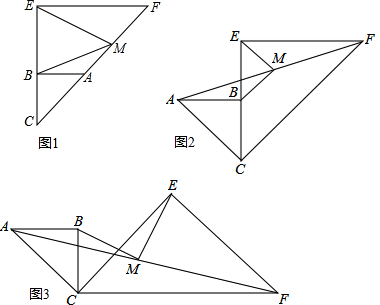
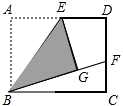（1）如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD于F点，若CF=1，FD=2，则BC的长为2$\sqrt{6}$．
E是正方形ABCD的对角线BD上一点，EF⊥BC，EG⊥CD，垂足分别是F、G．求证：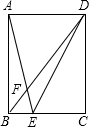
如图，在矩形ABCD中，AB=12，AD=9，点E是边BC上一点，连接AE，BD相交于点F，连接DE，若sin∠DEC=$\frac{2\sqrt{5}}{5}$，则BF=$\frac{15}{4}$．