题目内容
15.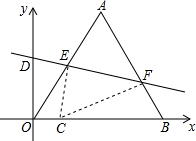 在平面直角坐标系中,等边三角形OAB的边长是2$\sqrt{3}$,且OB边落在x轴的正半轴上,点A落在第一象限.将△OAB沿直线y=kx+b折叠,使点A落在x轴上,设点C是点A落在x轴上的对应点.
在平面直角坐标系中,等边三角形OAB的边长是2$\sqrt{3}$,且OB边落在x轴的正半轴上,点A落在第一象限.将△OAB沿直线y=kx+b折叠,使点A落在x轴上,设点C是点A落在x轴上的对应点. (1)如果点A恰好落在点C(0,0),求b的值;
(2)设点C的横坐标为m,求b与m之间的函数关系式;
(3)直接写出当b=$\frac{1}{2}$时,点C的坐标.
分析 (1)根据等边三角形的性质,知如果点A恰好落在点C(0,0),则直线过点B.设直线和y轴的交点是M,则根据30°的直角三角形的性质即可求得b的值.
(2)连接AD、DC,可知AD=CD,根据勾股定理列方程得到b、m的关系式;
(3)当b=$\frac{1}{2}$时,代入(2)中m、b的关系式,求出C点坐标.
解答 解:(1)根据等边三角形的三线合一的性质,则此时直线过点B.
设直线和y轴的交点是M,
在Rt△CBM中,∠CBM=30°,OB=2$\sqrt{3}$,
则OM=2,即b=2.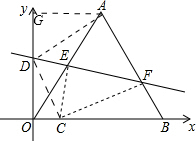 (2)如图,连接AD、DC,可知AD=CD,
(2)如图,连接AD、DC,可知AD=CD,
Rt△OCD中,CD2=OC2+OD2=m2+b2①,
Rt△ADG中,
AD2=DG2+AG2=($\sqrt{3}$)2+(3-b)2②,
由①、②得m2+6b-12=0,
∴b=2-$\frac{{m}^{2}}{6}$.
(3)当b=$\frac{1}{2}$时,2-$\frac{1}{6}$m2=$\frac{1}{2}$,解得m=±3;
故点C的坐标为(3,0)或(-3,0).
点评 此题考查了一次函数的综合题目,涉及到图形的翻折变换、直角三角形的边角关系、勾股定理等综合应用等知识,有一定难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.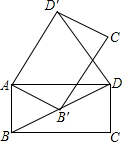 如图,在矩形ABCD中,AB=1,BC=$\sqrt{3}$.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
如图,在矩形ABCD中,AB=1,BC=$\sqrt{3}$.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
 如图,在矩形ABCD中,AB=1,BC=$\sqrt{3}$.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
如图,在矩形ABCD中,AB=1,BC=$\sqrt{3}$.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$+1 | D. | 2 |
 E是正方形ABCD的对角线BD上一点,EF⊥BC,EG⊥CD,垂足分别是F、G.求证:
E是正方形ABCD的对角线BD上一点,EF⊥BC,EG⊥CD,垂足分别是F、G.求证:
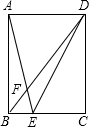 如图,在矩形ABCD中,AB=12,AD=9,点E是边BC上一点,连接AE,BD相交于点F,连接DE,若sin∠DEC=$\frac{2\sqrt{5}}{5}$,则BF=$\frac{15}{4}$.
如图,在矩形ABCD中,AB=12,AD=9,点E是边BC上一点,连接AE,BD相交于点F,连接DE,若sin∠DEC=$\frac{2\sqrt{5}}{5}$,则BF=$\frac{15}{4}$.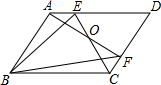 如图,在?ABCD中.E,F分别是AD,CD上,AF与CE交于点O,有下列命题:
如图,在?ABCD中.E,F分别是AD,CD上,AF与CE交于点O,有下列命题: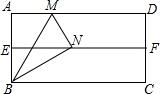 数学兴趣小组开展以下折纸活动:
数学兴趣小组开展以下折纸活动: