题目内容
2.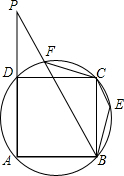 如图,E、F是正方形ABCD外接圆上的两个点,且∠EBF=45°,AD与BF的延长线交于点P,求证:
如图,E、F是正方形ABCD外接圆上的两个点,且∠EBF=45°,AD与BF的延长线交于点P,求证:(1)EC∥BP;
(2)BP•BE=$\sqrt{2}$AB2.
分析 (1)根据已知条件得到$\widehat{CAB}$的度数=270°,由圆周角定理得到∠E=$\frac{1}{2}$×270°=135°,证得∠E+∠EBF=180°,根据平行线的判定定理即可得到结论;
(2)连接BD,根据正方形的性质得到∠ADB=45°,BD=$\sqrt{2}$AB,AP∥BC,AB=BC,根据邻补角的定义得到∠PDB=135°,根据平行线的性质得到∠P=∠PBC=∠ECB,推出△PBD∽△BCE,根据相似三角形的性质得到$\frac{PB}{BC}=\frac{BD}{BE}$,等量代换即可得到结论.
解答 证明:(1)∵四边形ABCD是正方形,
∴$\widehat{CAB}$的度数=270°,
∴∠E=$\frac{1}{2}$×270°=135°,
∵∠EBF=45°,
∴∠E+∠EBF=180°,
∴EC∥BP;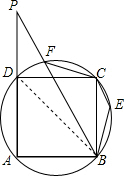
(2)连接BD,
∵四边形ABCD是正方形,
∴∠ADB=45°,BD=$\sqrt{2}$AB,AP∥BC,AB=BC,
∴∠PDB=135°,
∴∠PDB=∠E,
∵AP∥BC,CE∥PB,
∴∠P=∠PBC=∠ECB,
∴△PBD∽△BCE,
∴$\frac{PB}{BC}=\frac{BD}{BE}$,
∴$\frac{PB}{AB}=\frac{\sqrt{2}AB}{BE}$,
∴BP•BE=$\sqrt{2}$AB2.
点评 本题考查了相似三角形的判定和性质,正方形的性质等腰直角三角形的性质,平行线的判定和性质,连接BD构造相似三角形是解题的关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
17.下列各图经过折叠后不能围成一个正方体的是( )
| A. |  | B. |  | C. |  | D. |  |
11.下列图形是轴对称图形的是( )
| A. | 人的两点手 | B. | 两个1圆硬币 | C. | 线段 | D. | 平行四边形 |
12.实数-8的相反数是( )
| A. | 4 | B. | 8 | C. | -8 | D. | 0 |
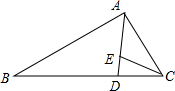 如图,在△ABC中,若∠DAC=∠B.
如图,在△ABC中,若∠DAC=∠B.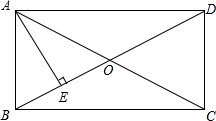 如图,在矩形ABCD中,AE⊥BD,垂足为E,BE与ED的长度之比为1:3,则tan∠ADB=$\frac{\sqrt{3}}{3}$.
如图,在矩形ABCD中,AE⊥BD,垂足为E,BE与ED的长度之比为1:3,则tan∠ADB=$\frac{\sqrt{3}}{3}$.