题目内容
14.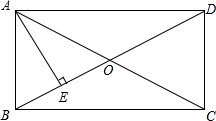 如图,在矩形ABCD中,AE⊥BD,垂足为E,BE与ED的长度之比为1:3,则tan∠ADB=$\frac{\sqrt{3}}{3}$.
如图,在矩形ABCD中,AE⊥BD,垂足为E,BE与ED的长度之比为1:3,则tan∠ADB=$\frac{\sqrt{3}}{3}$.
分析 由矩形的性质得出∠BAD=90°,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,得出OA=OB,再由已知条件得出OA=OB=AB,得出AB=$\frac{1}{2}$BD,证出∠ADB=30°,即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=90°,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
∵BE与ED的长度之比为1:3,
∴BE=OE,
∵AE⊥BD,
∴AB=OA,
∴OA=OB=AB,
∴AB=$\frac{1}{2}$BD,
∴∠ADB=30°,
∴tan∠ADB=$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题考查了矩形的性质、解直角三角形、线段垂直平分线的性质;熟练掌握矩形的性质,证出∠ADB=30°是解决问题的关键.

练习册系列答案
相关题目
5.在一次同学聚会时,大家一见面就相互握手,大家一共握了10次手,设参加这次聚会的同学共 有x人,根据题意得方程( )
| A. | x(x-1)=10 | B. | x(x+1)=10 | C. | $\frac{1}{2}$x(x-1)=10 | D. | $\frac{1}{2}$x(x+1)=10 |
6.在实数:-(-3.14159),1.010010001…,-(-1)2013,$-|{-\frac{3}{4}}|$,$4.\stackrel{•}2\stackrel{•}1$,$\frac{π}{3}$,$\frac{22}{7}$中,正分数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.如果规定收入为正,支出为负.收入500元记作+500元,那么支出400元应记作( )
| A. | -500元 | B. | -400元 | C. | 500元 | D. | 400元 |
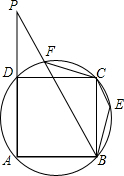 如图,E、F是正方形ABCD外接圆上的两个点,且∠EBF=45°,AD与BF的延长线交于点P,求证:
如图,E、F是正方形ABCD外接圆上的两个点,且∠EBF=45°,AD与BF的延长线交于点P,求证: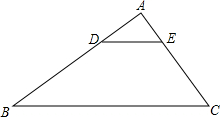 如图,在△ABC中,D为AB上一点且DE∥BC,交AC于点E,AD:AB=1:3,AC=6,BC=12.求:
如图,在△ABC中,D为AB上一点且DE∥BC,交AC于点E,AD:AB=1:3,AC=6,BC=12.求: 如图,已知AB是⊙O的直径,CD⊥AB,垂足为D,AE⊥AB,且AE=AC,BE交⊙O于点F.求证:EF•EB=AD•AB.
如图,已知AB是⊙O的直径,CD⊥AB,垂足为D,AE⊥AB,且AE=AC,BE交⊙O于点F.求证:EF•EB=AD•AB.