题目内容
 如图,已知点D在线段BE上,且
如图,已知点D在线段BE上,且| AB |
| AD |
| BC |
| DE |
| AC |
| AE |
考点:相似三角形的判定与性质
专题:证明题
分析:直接利用:三边对应成比例,则两个三角形相似这一判定定理得到△ABC∽△ADE,进而利用四点共圆的判定,圆的性质等知识即可解决问题.
解答:解:∵
=
=
,∴△ABC∽△ADE,
故∠ACB=∠AEB,点A、B、C、E共圆,
∴∠EBC=∠CAE.

| AB |
| AD |
| BC |
| DE |
| AC |
| AE |
故∠ACB=∠AEB,点A、B、C、E共圆,
∴∠EBC=∠CAE.

点评:考查了相似三角形的判定与性质的应用问题;同时还渗透了对四点共圆及其应用等知识的考查.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
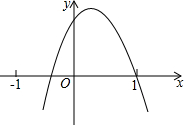 如图,抛物线y=ax2+bx+c的开口向下,交x轴的正半轴于(1,0),则下列结论错误的是( )
如图,抛物线y=ax2+bx+c的开口向下,交x轴的正半轴于(1,0),则下列结论错误的是( )| A、abc<0 |
| B、a-b+c<0 |
| C、2a+b>0 |
| D、a+c<0 |
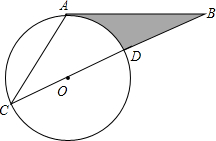 如图所示,AB相切⊙O于点A,直线BO交⊙O于点C、D,且OD=BD,AB=3
如图所示,AB相切⊙O于点A,直线BO交⊙O于点C、D,且OD=BD,AB=3 已知,在正方形ABCD中,⊙O与正方形的边AB、AD相切,对角线BD交⊙O与M、N两点,且MN=2
已知,在正方形ABCD中,⊙O与正方形的边AB、AD相切,对角线BD交⊙O与M、N两点,且MN=2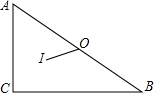 如图,△ABC中,∠C=90°,AC=3,BC=4,O为△ABC的外心,I为△ABC的内心,求OI的长.
如图,△ABC中,∠C=90°,AC=3,BC=4,O为△ABC的外心,I为△ABC的内心,求OI的长.