题目内容
12. 利用一面长18米的墙,另三边用30米长的篱笆围成一个面积为100平方米的矩形场地,求矩形的长和宽.
利用一面长18米的墙,另三边用30米长的篱笆围成一个面积为100平方米的矩形场地,求矩形的长和宽.
分析 设矩形场地的长为x米,那么宽为(30-x)÷2米,然后根据矩形面积公式列方程求解即可解决问题
解答 解:设矩形场地的长为x米,
由题意列方程得x×$\frac{30-x}{2}$=100,
整理得x2-30x+200=0,
解得:x1=20,x2=10.
又∵墙面长为18米,
∴x=20不符合题意,应舍去.
∴x=10.
答:围成的花圃的长和宽都是10米.
点评 本题考查的是一元二次方程的应用,要会把实际问题的数量关系转化成一元二次方程的问题解决,难度一般.

练习册系列答案
相关题目
1. 某艺术类学校进行绘画特长生的招生工作,每名考生需要参加“素描”“色彩”“速写”三个项目的测试,三个项目的满分均为100分,“素描”“色彩”“速写”按照4:4:2的比例计算得到选手最终成就,现有20名考生报名参加测试,测试结束后,考生的素描成绩如下(单位:分):
某艺术类学校进行绘画特长生的招生工作,每名考生需要参加“素描”“色彩”“速写”三个项目的测试,三个项目的满分均为100分,“素描”“色彩”“速写”按照4:4:2的比例计算得到选手最终成就,现有20名考生报名参加测试,测试结束后,考生的素描成绩如下(单位:分):
88,85,90,99,86,68,94,98,78,97
96,93,89,94,89,85,80,95,89,77
请根据上述数据,解决下列问题:
(1)补全下面考生素描成绩的表格(每组数据含最小值不含最大值)和频数分布直方图;
(2)如表为甲、乙两名选手比赛成绩的记录表,现要在甲、乙二人中录取一名,请通过计算得出谁最终被录取.
 某艺术类学校进行绘画特长生的招生工作,每名考生需要参加“素描”“色彩”“速写”三个项目的测试,三个项目的满分均为100分,“素描”“色彩”“速写”按照4:4:2的比例计算得到选手最终成就,现有20名考生报名参加测试,测试结束后,考生的素描成绩如下(单位:分):
某艺术类学校进行绘画特长生的招生工作,每名考生需要参加“素描”“色彩”“速写”三个项目的测试,三个项目的满分均为100分,“素描”“色彩”“速写”按照4:4:2的比例计算得到选手最终成就,现有20名考生报名参加测试,测试结束后,考生的素描成绩如下(单位:分):88,85,90,99,86,68,94,98,78,97
96,93,89,94,89,85,80,95,89,77
请根据上述数据,解决下列问题:
(1)补全下面考生素描成绩的表格(每组数据含最小值不含最大值)和频数分布直方图;
| 分组 | 人数(频数) |
| 60-70 | 1 |
| 70-80 | 2 |
| 80-90 | 9 |
| 90-100 | 8 |
| 合计 | 20 |
| 项目 成绩 | 素描 | 色彩 | 速写 |
| 甲 | 98 | 93 | 95 |
| 乙 | 95 | 95 | 100 |
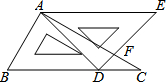 将一副学生用的三角板按如图所示的方式摆放,若AE∥BC,则∠AFD的度数是75°.
将一副学生用的三角板按如图所示的方式摆放,若AE∥BC,则∠AFD的度数是75°.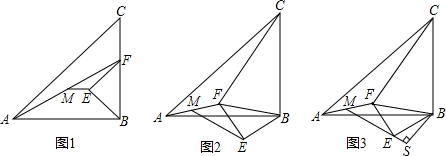
 如图,在一面靠墙的空地商用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.
如图,在一面靠墙的空地商用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.