题目内容
20.把一根24cm长的铁丝分成两段,将每一段围成一个正方形,若这两个正方形的面积之差是12cm2,则所分成的两段铁丝中较长的是16cm.分析 设其中较大的一段的长为xcm(x≥10),则另一段的长为(24-x)cm,根据两个正方形的面积之和为12cm2建立方程求出其解即可.
解答 解:设其中较大的一段的长为xcm(x≥12),则另一段的长为(24-x)cm.
则两个小正方形的边长分别为$\frac{1}{4}$x cm和$\frac{1}{4}$(24-x)cm
∵两正方形面积之差为12cm2,
∴($\frac{1}{4}$x)2-[$\frac{1}{4}$(24-x)]2=12,
解得x=16cm.则另一段长为24-16=8cm.
∴两段铁丝中较长的为16cm.
故答案是:16.
点评 本题考查了正方形的面积公式的运用,列一元二次方程解实际问题的运用,一元二次方程的解法的运用,解答时两个正方形的面积之和为12cm2建立方程是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.体育达标测试中,有8名男生“30秒跳绳”的成绩(单位:次)分别是:140,120,100,80,90,160,120,70,这组数据的中位数和众数分别是( )
| A. | 100,120 | B. | 120,110 | C. | 110,120 | D. | 120,120 |
 利用一面长18米的墙,另三边用30米长的篱笆围成一个面积为100平方米的矩形场地,求矩形的长和宽.
利用一面长18米的墙,另三边用30米长的篱笆围成一个面积为100平方米的矩形场地,求矩形的长和宽.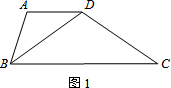 我们把有一组邻边相等,一组对边平行但不相等的四边形称作“准菱形”.
我们把有一组邻边相等,一组对边平行但不相等的四边形称作“准菱形”.