题目内容
5．
如图，在等腰Rt△ABC中，∠C=90°，AC=3，D是边AC上一点，若tan∠DBA=$\frac{1}{5}$，求AD的值．
分析 作DE⊥AB于E，先根据腰直角三角形的性质得到AB=$\sqrt{2}$AC=3$\sqrt{2}$，∠A=45°，设AE=x，则DE=x，AD=$\sqrt{2}$x，在Rt△BED中，利用∠DBE的正切得到BE=5x，然后由AE+BE=AB可计算出x=$\frac{\sqrt{2}}{2}$，再利用AD=$\sqrt{2}$x进行计算．
解答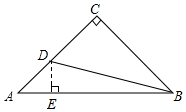 
解：作DE⊥AB于E，如图，
∵△ACB为等腰直角三角形，∠C=90°，
∴BC=AC=3，∠A=45°，
∴AB=$\sqrt{2}$AC=3$\sqrt{2}$，
在Rt△ADE中，设AE=x，则DE=x，AD=$\sqrt{2}$x，
在Rt△BED中，tan∠DBE=tan∠DBA=$\frac{DE}{BE}$=$\frac{1}{5}$，
∴BE=5x，
∴AB=AE+BE=x+5x=3$\sqrt{2}$，解得x=$\frac{\sqrt{2}}{2}$，
∴AD=$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=1．
故AD的值为1．
点评 本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．也考查了等腰直角三角形的性质．
练习册系列答案
相关题目
二次函数 y=ax2+bx+c（a≠0）的图象经过点A（4，0），B（2，8），且以x=1为对称轴．
如图，在△ABC中，DE∥BC交AB、AC于点D、E，AE=3，AC=5，DE=4，那么BC=$\frac{20}{3}$．
如图，在△ABC中，AC=4，BC边上的垂直平分线DE分别交BC、AB于点D、E，若△AEC的周长是14，则直线DE上任意一点到A、C距离和最小为（ ）