题目内容
9．如图，下列图形都是由面积为1的正方形按照一定的规律组成的，第（1）个图形中面积为1的正方形有2个，第（2）个图形中面积为1的正方形有5个，第（3）个图形中面积为1的正方形有9个，…，按此规律，则第（20）个图形中面积为1的正方形的个数是230．
分析 由图形可知：第（1）个图形中面积为1的正方形有2个，第（2）个图形中面积为1的图象有2+3=5个，第（3）个图形中面积为1的正方形有2+3+4=9个，…，按此规律，第n个图形中面积为1的正方形有2+3+4+…+n+1=$\frac{n（n+3）}{2}$，进一步求得第（20）个图形中面积为1的正方形的个数即可．
解答 解：第（1）个图形中面积为1的正方形有2个，
第（2）个图形中面积为1的图象有2+3=5个，
第（3）个图形中面积为1的正方形有2+3+4=9个，
…，
按此规律，
第n个图形中面积为1的正方形有2+3+4+…+（n+1）=$\frac{n（n+3）}{2}$个，
则第（20）个图形中面积为1的正方形的个数为2+3+4+5+6+…+21=230个．
故答案为：230．
点评 此题考查图形的变化规律，找出图形与数字之间的运算规律，利用规律解决问题．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
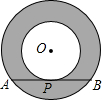如图，半径均为整数的同心圆组成的“圆环带”，若大圆的弦AB与小圆相切于点P，且弦AB的长度为定值$4\sqrt{3}$，则满足条件的不全等的“圆环带”有（ ）
在△ABC中，AC的垂直平分线交AC于E，交BC于D，△ABC的周长是17cm，AC=5cm，△ABD的周长是12cm．
如图所示，在△ABC中，O为∠ABC，∠ACB的平分线的交点，如果OD⊥AB，OE⊥AC，OF⊥BC，垂足分别为D，E，F，OD与OE是否相等？为什么？
如图，∠AOB内有一点P：
为缓解交通拥堵，某区拟计划修建一地下通道，该通道一部分的截面如图所示（图中地面AD与通道BC平行），通道水平宽度BC为8米，∠BCD=135°，通道斜面CD的长为6米，通道斜面AB的坡度i=1：$\sqrt{2}$．