题目内容
8.从-4,-1,0,1这四个数中,任选两个不同的数分别作为m,n的值,恰好使得关于x的不等式组$\left\{\begin{array}{l}{2x+1≥m}\\{2-3x≥n}\end{array}\right.$有3个整数解,且点(m,n)落在双曲线y=-$\frac{4}{x}$上的概率为$\frac{1}{6}$.分析 首先用列表法或树形图得到所用可能的情况,若使点(m,n)落在双曲线y=-$\frac{4}{x}$上,则mn=-4,由此得到mn的关系式,再根据恰好使得关于x,y的二元一次方程组$\left\{\begin{array}{l}{2x+1≥m}\\{2-3x≥n}\end{array}\right.$有3个整数解,即可求出m,n的值,由此可得到点(m,n)落在双曲线y=-$\frac{4}{x}$上的概率.
解答 解:画树状图得:
若使点(m,n)落在双曲线y=-$\frac{4}{x}$上,则mn=-4,
∴点(m,n)可以是(1,-4)、(-4,1),
∵恰好使得关于x,y的二元一次方程组$\left\{\begin{array}{l}{2x+1≥m}\\{2-3x≥n}\end{array}\right.$有3个整数解,
∴点(m,n)可以是(1,-4)、(-4,1),
∴且点(m,n)落在双曲线y=-$\frac{4}{x}$上的概率为$\frac{2}{12}$=$\frac{1}{6}$,
故答案为:$\frac{1}{6}$.
点评 此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
18.下列各式中,计算正确的是( )
| A. | (a+4)(a-4)=a2-4 | B. | (2a+3)(2a-3)=2a2-9 | ||
| C. | (5ab+1)(5ab-1)=25a2b2-1 | D. | (a+2)(a-4)=a2-8 |
16.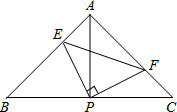 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于E、F.给出以下四个结论:①AF=BE;②△EPF是等腰直角三角形;③S四边形AEPF=$\frac{1}{2}$S△ABC;④EF2=BE2+CF2.( )
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于E、F.给出以下四个结论:①AF=BE;②△EPF是等腰直角三角形;③S四边形AEPF=$\frac{1}{2}$S△ABC;④EF2=BE2+CF2.( )
 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于E、F.给出以下四个结论:①AF=BE;②△EPF是等腰直角三角形;③S四边形AEPF=$\frac{1}{2}$S△ABC;④EF2=BE2+CF2.( )
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于E、F.给出以下四个结论:①AF=BE;②△EPF是等腰直角三角形;③S四边形AEPF=$\frac{1}{2}$S△ABC;④EF2=BE2+CF2.( )| A. | ②③ | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
3.用一个半径为6cm的半圆围成一个圆锥的侧面,则这个圆锥的表面积为( )cm2.
| A. | 6π+6 | B. | 12π | C. | 27π | D. | 18π |
13.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:
下列说法不正确的是( )
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
| A. | x与y都是变量,且x是自变量,y是因变量 | |
| B. | 物体质量每增加1kg,弹簧长度y增加0.5cm | |
| C. | y与x的关系表达式是y=0.5x | |
| D. | 所挂物体质量为7kg时,弹簧长度为13.5cm |
20. 在菱形ABCD中,下列结论错误的是( )
在菱形ABCD中,下列结论错误的是( )
 在菱形ABCD中,下列结论错误的是( )
在菱形ABCD中,下列结论错误的是( )| A. | BO=DO | B. | ∠DAC=∠BAC | C. | AC⊥BD | D. | AO=DO |