题目内容
16.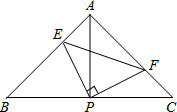 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于E、F.给出以下四个结论:①AF=BE;②△EPF是等腰直角三角形;③S四边形AEPF=$\frac{1}{2}$S△ABC;④EF2=BE2+CF2.( )
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于E、F.给出以下四个结论:①AF=BE;②△EPF是等腰直角三角形;③S四边形AEPF=$\frac{1}{2}$S△ABC;④EF2=BE2+CF2.( )| A. | ②③ | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
分析 通过证明△AFP≌△BEP就可以得出AF=BE,EP=PF,得出AE=CF,得出△EPF是等腰直角三角形,由S四边形AEPF=S△APE+S△APF.就可以得出S四边形AEPF=S△CPF+S△APF,就可以得出结论,由AF=BE,AE=CF得出EF2=BE2+CF2.
解答 解:∵AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,
∴∠B=∠PAF=45°,BP=AP,
∵∠APE+∠BPE=90°,∠APE+∠APF=90°,
∴∠BPE=∠APF.
在△BPE和△APF中,
$\left\{\begin{array}{l}{∠B=∠PAF}\\{BP=AP}\\{∠BPE=∠APF}\end{array}\right.$,
∴△AFP≌△BEP(ASA),
∴BE=AF,PE=PF,
故①AF=BE;②△EPF是等腰直角三角形正确;
∵EPF=90°,在Rt△EPF中,由勾股定理,得
EF2=PE2+PF2,
∴EF2=BE2+CF2.故④正确;
∵S四边形AEPF=S△APE+S△APF.
∴S四边形AEPF=S△CPF+S△APF=S△FAE=$\frac{1}{2}$S△ABC.故③正确.
故选D.
点评 本题考查了等腰直角三角形的性质的运用,全等三角形的判定及性质的运用,中位线的性质的运用,等腰直角三角形的判定定理的运用,三角形面积公式的运用,解答时灵活运用等腰直角三角形的性质求解是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下面生活中的物体的运动情况可以看成平移的是( )
(1)摆动的钟摆. (2)在笔直的公路上行驶的汽车. (3)随风摆动的旗帜. (4)摇动的大绳. (5)汽车玻璃上雨刷的运动. (6)从楼顶自由落下的球(球不旋转).
(1)摆动的钟摆. (2)在笔直的公路上行驶的汽车. (3)随风摆动的旗帜. (4)摇动的大绳. (5)汽车玻璃上雨刷的运动. (6)从楼顶自由落下的球(球不旋转).
| A. | (1)(2) | B. | (1)(3)(4) | C. | (3)(4)(5) | D. | (2)(6) |
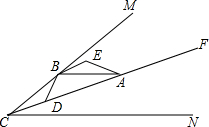 已知CA平分∠MCN,AB∥CN,点D是线段CA上任一点,且BD=BE,∠DBE=∠CBA,连AE,DE
已知CA平分∠MCN,AB∥CN,点D是线段CA上任一点,且BD=BE,∠DBE=∠CBA,连AE,DE