题目内容
已知A、B是平面直角坐标系中的两点,A、B两点的坐标分别为(
,4)和(-
,1),在x轴上是否存在一点P,使得P到A、B的距离之和最小?若存在,请求出最小距离;若不存在,请说明理由.
| 2 |
| 2 |
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:过点B作点B关于x轴的对称点B′,连接AB′交x轴于点P,则点P即为所求点,AB′的长为P到A、B的距离之和的最小值.
解答: 解:存在.
解:存在.
如图所示,过点B作点B关于x轴的对称点B′,连接AB′交x轴于点P,则点P即为所求点,AB′的长为P到A、B的距离之和的最小值.
∵A、B两点的坐标分别为(
,4)和(-
,1),
∴B′D=|
+
|=2
,AD=4+1=5,
∴AB′=
=
=
,即P到A、B的距离之和的最小值为
.
 解:存在.
解:存在.如图所示,过点B作点B关于x轴的对称点B′,连接AB′交x轴于点P,则点P即为所求点,AB′的长为P到A、B的距离之和的最小值.
∵A、B两点的坐标分别为(
| 2 |
| 2 |
∴B′D=|
| 2 |
| 2 |
| 2 |
∴AB′=
| B′D2+AD2 |
(2
|
| 33 |
| 33 |
点评:本题考查的是轴对称-最短路线问题,熟知“两点之间,线段最短”是解答此题的关键.

练习册系列答案
相关题目
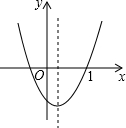 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则c、△(△=b2-4ac)与零的大小关系是c
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则c、△(△=b2-4ac)与零的大小关系是c 如图,在Rt△ABC中,∠ACB=90°,CA=CB,如果斜边AB=5cm,那么斜边上的高CD=
如图,在Rt△ABC中,∠ACB=90°,CA=CB,如果斜边AB=5cm,那么斜边上的高CD=