题目内容
14.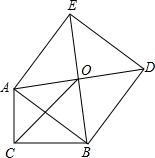 如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=$\frac{5}{6}$,OC=$\sqrt{2}$,则另一直角边BC的长为$\frac{7}{6}$.
如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=$\frac{5}{6}$,OC=$\sqrt{2}$,则另一直角边BC的长为$\frac{7}{6}$.
分析 过点O作OM⊥CA,交CA的延长线于点M,作ON⊥BC于点N.只要证明△OMA≌△ONB推出OM=ON,MA=NB推出O点在∠ACB的平分线上,推出△OCM为等腰直角三角形.由OC=$\sqrt{2}$,推出CM=ON=1.推出MA=CM-AC=1-$\frac{5}{6}$=$\frac{1}{6}$,可得BC=CN+NB=1+$\frac{1}{6}$=$\frac{7}{6}$.
解答 解:过点O作OM⊥CA,交CA的延长线于点M,作ON⊥BC于点N.
∵四边形ABCD是正方形,
∴OA=OB,∠AOB=90°,
∵∠MON=∠AOB=90°,
∴∠AOM=∠BON,
在△AOM和△BON中,
$\left\{\begin{array}{l}{∠OMA=∠ONB}\\{∠AOM=∠BON}\\{OA=OB}\end{array}\right.$
∴△OMA≌△ONB,
∴OM=ON,MA=NB.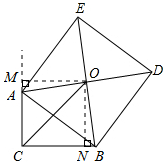
∴O点在∠ACB的平分线上,
∴△OCM为等腰直角三角形.
∵OC=$\sqrt{2}$,
∴CM=ON=1.
∴MA=CM-AC=1-$\frac{5}{6}$=$\frac{1}{6}$,
∴BC=CN+NB=1+$\frac{1}{6}$=$\frac{7}{6}$.
故答案为:$\frac{7}{6}$.
点评 此题考查了正方形的性质,全等三角形的判定与性质,勾股定理,以及等腰直角三角形的判定与性质、角平分线的判定,利用了转化及等量代换的思想,根据题意作出相应的辅助线是解本题的关键.

练习册系列答案
相关题目
5. 如图,l1∥l2,∠1=110°,则∠2的度数是( )
如图,l1∥l2,∠1=110°,则∠2的度数是( )
 如图,l1∥l2,∠1=110°,则∠2的度数是( )
如图,l1∥l2,∠1=110°,则∠2的度数是( )| A. | 70° | B. | 110° | C. | 120° | D. | 60° |
2.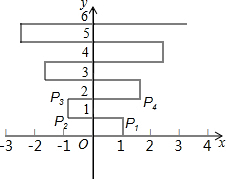 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,则点P第2017次跳动至P2017的坐标是( )
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,则点P第2017次跳动至P2017的坐标是( )
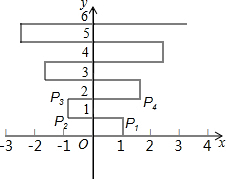 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,则点P第2017次跳动至P2017的坐标是( )
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,则点P第2017次跳动至P2017的坐标是( )| A. | (504,1007) | B. | (505,1009) | C. | (1008,1007) | D. | (1009,1009) |
3.已知$\left\{\begin{array}{l}{a+2b=4}\\{3a+2b=8}\end{array}\right.$,则2a+2b等于( )
| A. | 6 | B. | $\frac{16}{3}$ | C. | 4 | D. | 2 |
4.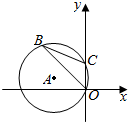 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上的一点,则cos∠OBC=( )
如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上的一点,则cos∠OBC=( )
 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上的一点,则cos∠OBC=( )
如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上的一点,则cos∠OBC=( )| A. | $\frac{1}{3}$ | B. | 2$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{2\sqrt{2}}{3}$ |
 如图,把一张长方形纸条ABCD沿AF折叠,已知∠ADB=20°,那么∠BAF应为多少度时,才能使AB′∥BD?
如图,把一张长方形纸条ABCD沿AF折叠,已知∠ADB=20°,那么∠BAF应为多少度时,才能使AB′∥BD?