题目内容
19. 如图,把一张长方形纸条ABCD沿AF折叠,已知∠ADB=20°,那么∠BAF应为多少度时,才能使AB′∥BD?
如图,把一张长方形纸条ABCD沿AF折叠,已知∠ADB=20°,那么∠BAF应为多少度时,才能使AB′∥BD?
分析 根据折叠的性质得到∠B′AF=∠BAF,要AB′∥BD,则要有∠B′AD=∠ADB=20°,从而得到∠B′AB=20°+90°=110°,即可求出∠BAF.
解答 解:∠BAF应为55度.
理由是:∵∠ADB=20°,四边形ABCD是长方形,
∴∠ABD=70°.
∵要使AB′∥BD,需使∠BAB′=110°,
由折叠可知∠BAF=∠B′AF,
∴∠BAF应为55度.
点评 本题考查了折叠的性质:折叠前后两图形全等,即对应角相等,对应线段相等.也考查了直线平行的判定.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
7.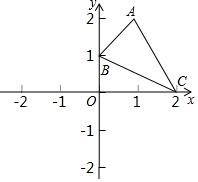 如图,在平面直角坐标系xOy中,A(1,2),B(0,1),C(2,0)若将△ABC平移到△A1B1C1,使点A1与原点重合,则点C1的坐标和△A1B1C1的面积分别是( )
如图,在平面直角坐标系xOy中,A(1,2),B(0,1),C(2,0)若将△ABC平移到△A1B1C1,使点A1与原点重合,则点C1的坐标和△A1B1C1的面积分别是( )
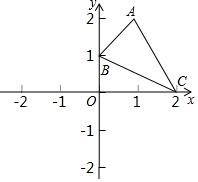 如图,在平面直角坐标系xOy中,A(1,2),B(0,1),C(2,0)若将△ABC平移到△A1B1C1,使点A1与原点重合,则点C1的坐标和△A1B1C1的面积分别是( )
如图,在平面直角坐标系xOy中,A(1,2),B(0,1),C(2,0)若将△ABC平移到△A1B1C1,使点A1与原点重合,则点C1的坐标和△A1B1C1的面积分别是( )| A. | C1(0,1),2 | B. | C1(0,1),1.5 | C. | C1(1,-2),2 | D. | C1(1,-2),1.5 |
4.下列各式是分式的是( )
| A. | $\frac{x}{2}$ | B. | $\frac{x}{π}$ | C. | $\frac{2}{x}$ | D. | $\frac{x+y}{2}$ |
11.在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017D2017的边长是( )


| A. | ($\frac{1}{2}$)2016 | B. | ($\frac{1}{2}$)2017 | C. | ($\frac{{\sqrt{3}}}{3}$)2016 | D. | ($\frac{{\sqrt{3}}}{3}$)2017 |
9.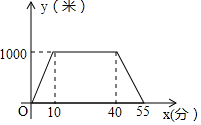 小明从家里出发到超市进行购物后返回,小明离开家的路程y(米)与所用时间x(分)之间的关系如图,则下列说法不正确的是( )
小明从家里出发到超市进行购物后返回,小明离开家的路程y(米)与所用时间x(分)之间的关系如图,则下列说法不正确的是( )
 小明从家里出发到超市进行购物后返回,小明离开家的路程y(米)与所用时间x(分)之间的关系如图,则下列说法不正确的是( )
小明从家里出发到超市进行购物后返回,小明离开家的路程y(米)与所用时间x(分)之间的关系如图,则下列说法不正确的是( )| A. | 小明家到超市的距离是1000米 | B. | 小明在超市购物的时间为30分钟 | ||
| C. | 小明离开家的时间共55分钟 | D. | 小明返回的速度比去时的速度快 |
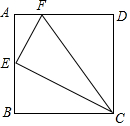 如图,已知正方形ABCD的边长为4,E为AB中点,F为AD上的一点,且AF=$\frac{1}{4}$AD,请你判断△EFC的形状并说明理由.
如图,已知正方形ABCD的边长为4,E为AB中点,F为AD上的一点,且AF=$\frac{1}{4}$AD,请你判断△EFC的形状并说明理由. 如图,在△ABC中,AB=AC,AD是BC边上的中线,O是AB的中点,延长DO至E,使OE=OD,连接AE、BE.
如图,在△ABC中,AB=AC,AD是BC边上的中线,O是AB的中点,延长DO至E,使OE=OD,连接AE、BE.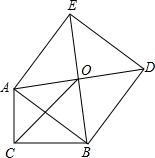 如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=$\frac{5}{6}$,OC=$\sqrt{2}$,则另一直角边BC的长为$\frac{7}{6}$.
如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=$\frac{5}{6}$,OC=$\sqrt{2}$,则另一直角边BC的长为$\frac{7}{6}$.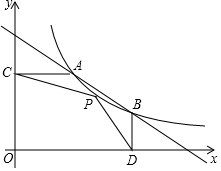 如图,A(n,n+1),B(n+3,n-1)是反比例函数y1=$\frac{k}{x}$(x>0)的图象与一次函数y2=ax+b图象的两个交点.求:
如图,A(n,n+1),B(n+3,n-1)是反比例函数y1=$\frac{k}{x}$(x>0)的图象与一次函数y2=ax+b图象的两个交点.求: